Geometric Thinking

Morley’s Triangle 莫利三角

Every center we’ve seen has been based on angle bisectors, altitudes, perpendicular bisectors, or medians. Let’s try one more kind of manipulation, this time with angle trisectors which divide an angle into three equal parts.
我们所见过的每个中心都是基于角度平分线、高度、垂直平分线或中位数的。让我们尝试另一种操作，这次使用 角度三等分 线，将一个角度分成 三个 相等的部分。

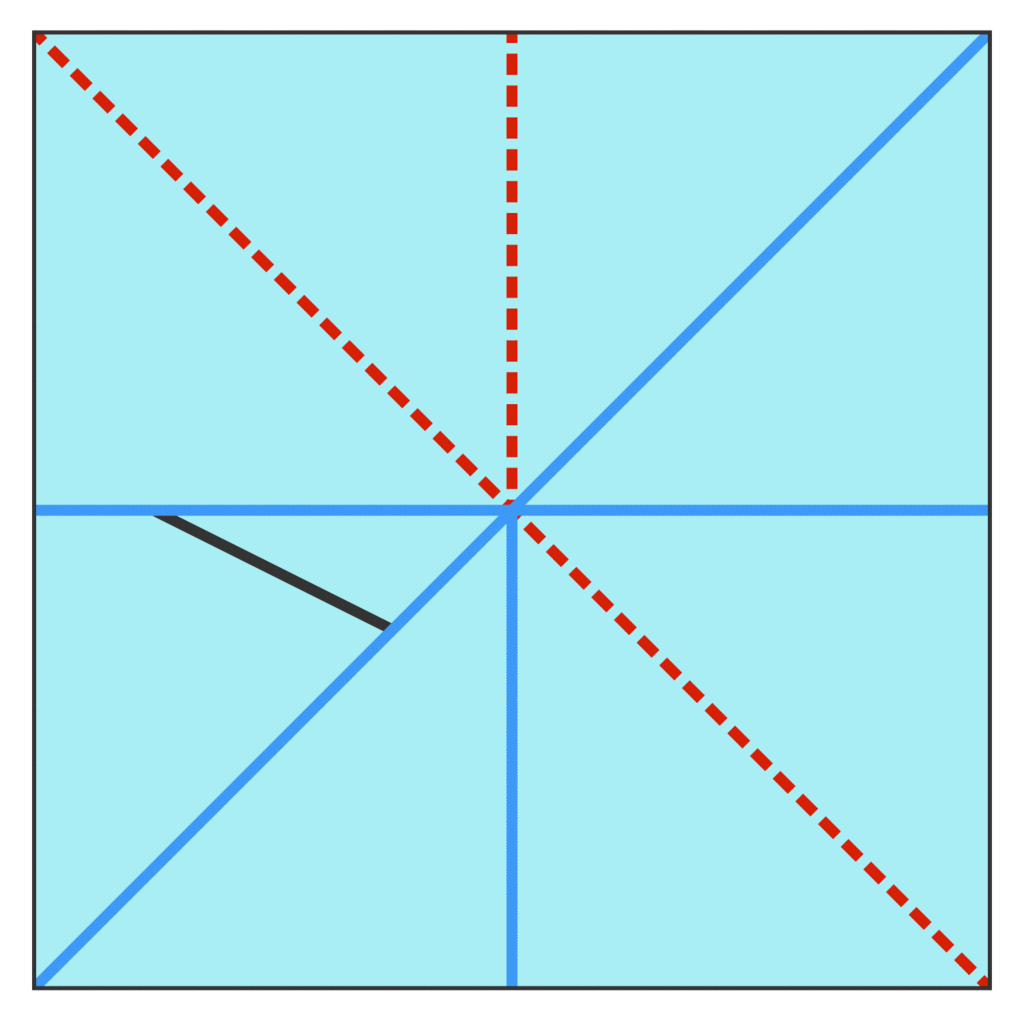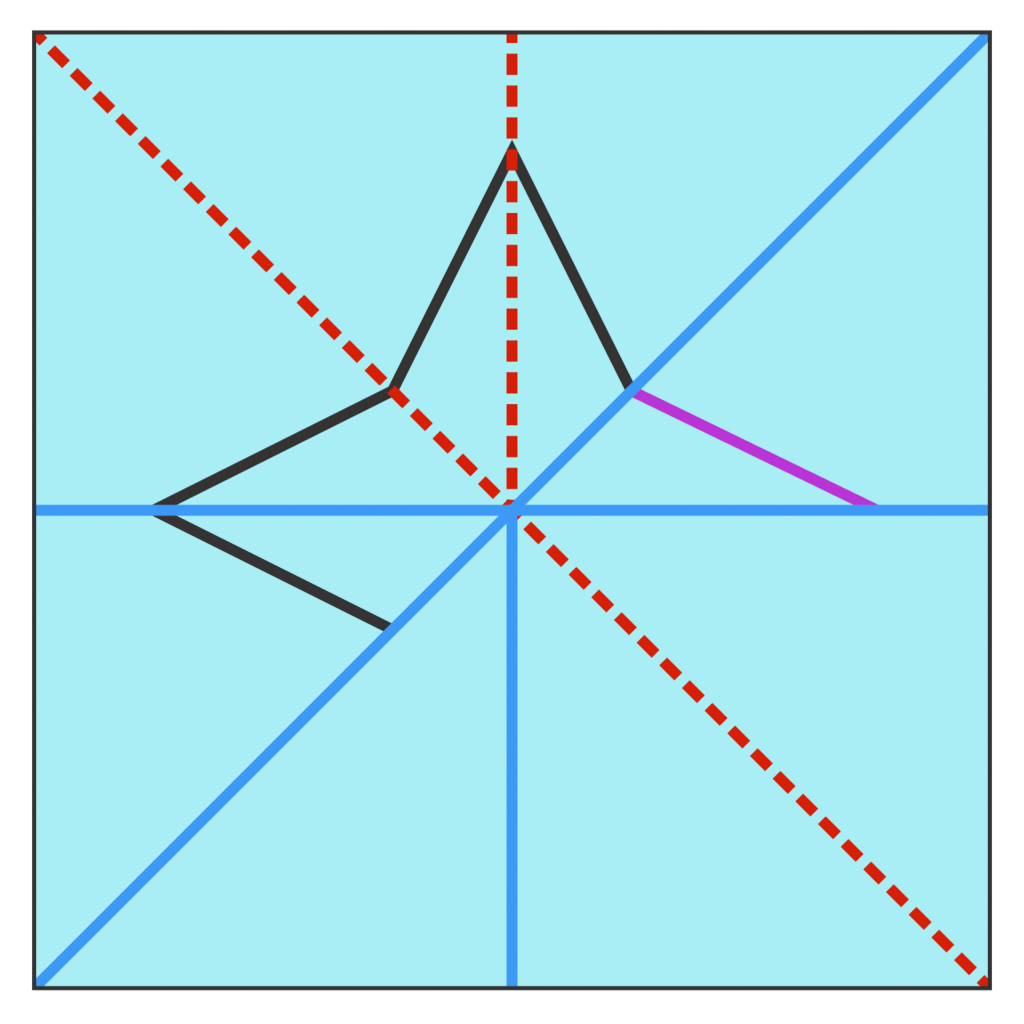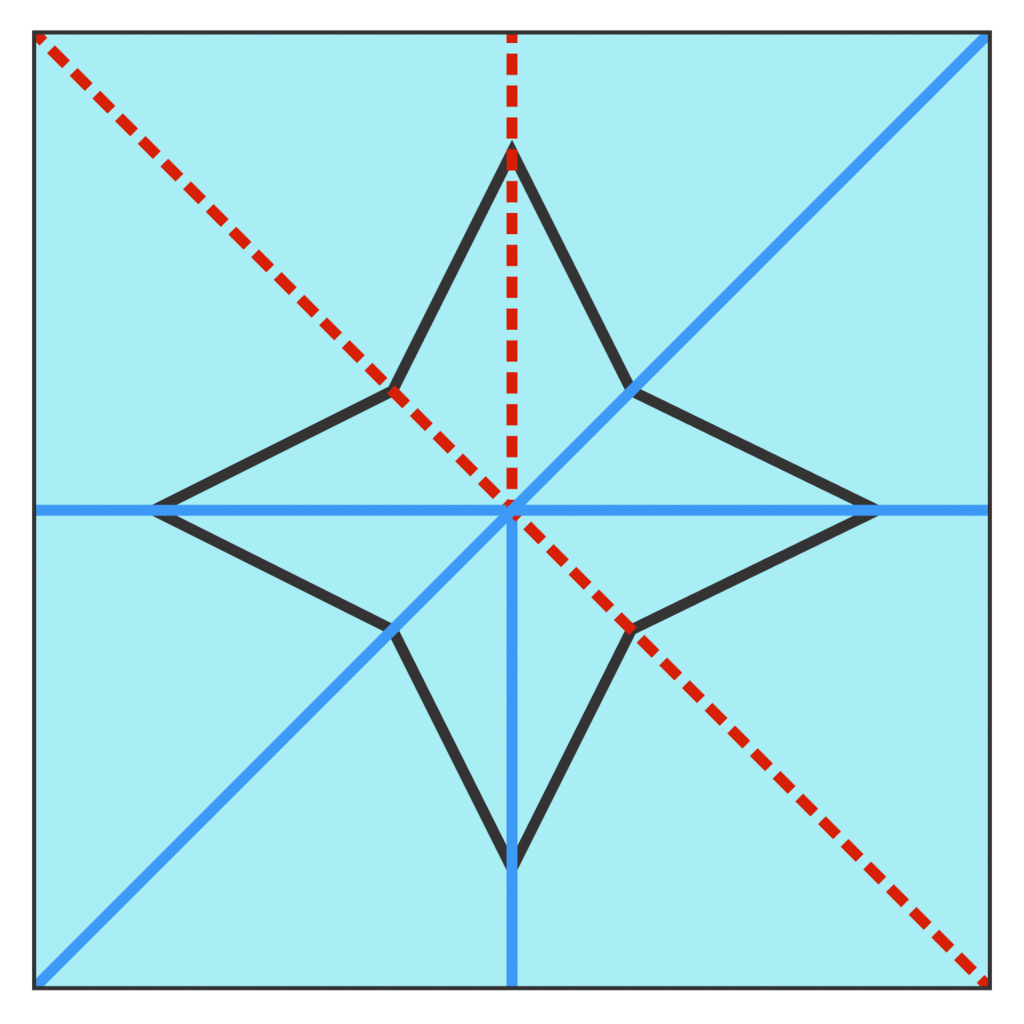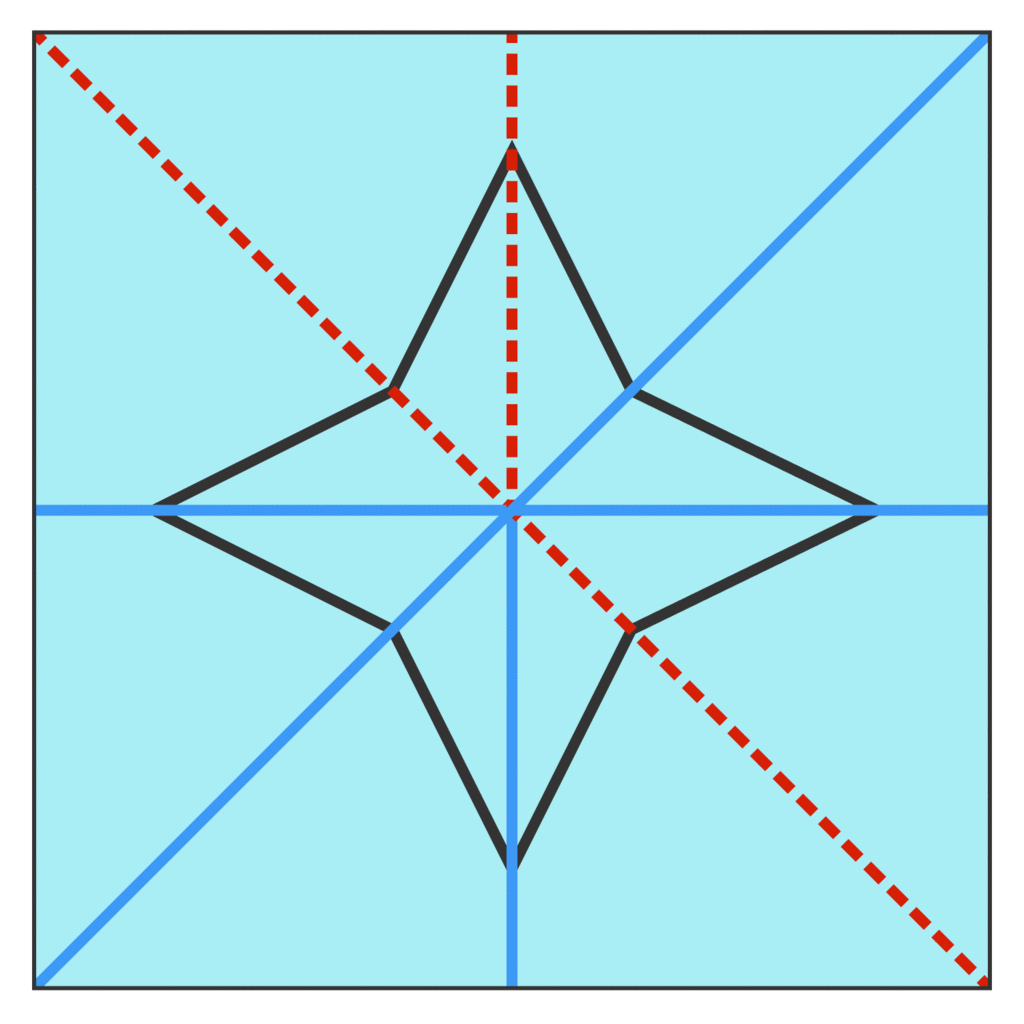
Take a triangle and draw in all the angle trisectors:
取一个三角形并绘制所有角度三分线：

If we stop the trisectors all at their first point of intersection, the trisectors don’t intersect at a single point but rather at three points.
如果我们在三等分线的第一个交点处停止它们，则三等分线不会在单个点相交，而是在三个点处相交。 The three points have a special relationship you can guess by looking at the diagram. What is it?
这三个点有一个特殊的关系，你可以通过查看图表来猜到。这是什么？

The points form a right triangle.
这些点形成一个直角三角形。

The points form a scalene triangle.
这些点形成一个斜角三角形。

The points form an equilateral triangle.
这些点形成一个等边三角形。

Explanation 解释

The points will form an equilateral triangle no matter the starting triangle:
无论起始三角形如何，这些点都将形成一个等边三角形：

This proof will come throughout the lesson — you may want to experiment with a few more triangles of your own before going on.
这个证明将贯穿整个课程 — 在继续之前，您可能想尝试更多自己的三角形。 We’d like to make the theorem:
我们想制作定理：

Starting from any triangle, draw in the angle trisectors — the first points that they intersect at form an equilateral triangle.
从任何三角形开始，绘制角三等分线 — 它们相交的第一个点形成一个 等边 三角形。

We’re going to take an unusual approach and run the process backward. We’ll start with an equilateral triangle and form a larger final triangle around it. We’re going to do it in a general way that allows us to form any final triangle, which means the angle trisectors of any triangle make an equilateral triangle.
我们将采用一种不寻常的方法，向后运行该过程。我们将从一个等边三角形开始，然后围绕它形成一个更大的最终三角形。我们将以一种通用的方式进行，允许我们形成 任何 最终的三角形，这意味着任何三角形的角三等分线都构成一个等边三角形。

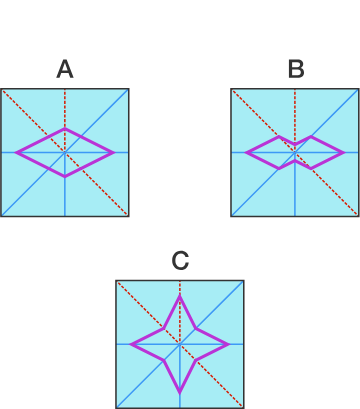
What’s the value of a+b+c?a+b+c?
a+b+c?a+b+c? 的值是多少

60∘60∘

90∘90∘

150∘150∘

180∘180∘

Explanation 解释

The overall large triangle is composed of a,a, b,b, and c,c, three times each, so we obtain
整个大三角形由 a,a, b,b, 和 c,c, 各 3 次组成，因此我们得到

3a+3b+3c=180∘.3a+3b+3c=180∘.

Divide both sides by 33 to get
将两侧除以 33 得到

a+b+c=60∘.a+b+c=60∘.

Begin by drawing an equilateral triangle XYZ,XYZ, and then replicate the triangle three times, as shown in blue:
首先绘制一个等边三角形 XYZ,XYZ, ，然后将三角形复制三次，如蓝色所示：

Now, pick any positive a,b,a,b, and cc that sum to 60∘.60∘. Remember this is a condition of our final triangle — also, because we can pick any set of a,b,a,b, and cc with the right sum, it allows for any valid final triangle we want:
现在，选择任何总 和为 60∘.60∘. 的正 a,b,a,b, 和 cc 请记住，这是我们最终三角形的条件——此外，因为我们可以选择任何具有正确和的 a,b,a,b, 和 cc 集合，它允许我们想要任何有效的最终三角形：

Put in line segments as shown, where the measures of the angles match the chosen numbers.
如图所示放入线段中，其中角度的测量值与所选数字匹配。 Put in line segments as shown, where the measures of the angles match the chosen numbers.
如图所示放入线段中，其中角度的测量值与所选数字匹配。

What’s the measure of ∠A?∠A?
∠A?∠A? 的度量是什么

aa

bb

cc

b+cb+c

If we look at △AYZ,△AYZ, we know that
如果我们看一下 △AYZ,△AYZ, 我们就知道

(60∘+c)+(60∘+b)+(?)=180∘.(60∘+c)+(60∘+b)+(?)=180∘.

Rearranging terms, we know b+c+(?)=60∘.b+c+(?)=60∘.
重新排列术语，我们知道 b+c+(?)=60∘.b+c+(?)=60∘.

Also, it’s still a condition that a+b+c=60∘,a+b+c=60∘, which implies b+c=60∘−a.b+c=60∘−a.
此外，它仍然是一个条件 a+b+c=60∘,a+b+c=60∘, ，这意味着 b+c=60∘−a.b+c=60∘−a.

We can now substitute (60∘−a)(60∘−a) in for (b+c)(b+c) in the equation b+c+(?)=60∘:b+c+(?)=60∘:
我们现在可以用 (60∘−a)(60∘−a) 代替 方程 b+c+(?)=60∘:b+c+(?)=60∘: 中的 (b+c)(b+c)

60∘−a+(?)=60∘.60∘−a+(?)=60∘.

Add aa to both sides and subtract 60∘60∘ from both sides:
在 两边加上 aa ，从两边减去 60∘60∘ ：

a=(?).a=(?).

The exact same logic used to determine that ∠A∠A measures aa can be applied to determine that ∠B∠B measures b:b:
用于确定 ∠A∠A 度量 aa 的完全相同的逻辑可用于确定 ∠B∠B 度量 b:b:

Now, our strategy is going to extend one side of the equilateral triangle and use similar triangles to keep filling in angles. Remember our goal picture will have the final triangle trisected with a,a, b,b, and cc being the individual smaller angles.
现在，我们的策略将延长等边三角形的一侧，并使用类似的三角形来继续填充角度。请记住，我们的目标图片将最后一个三角形分成三等分，其中 a,a, 、 b,b, 和 cc 是单独的较小角度。

Let’s extend one side of the blue equilateral triangle to new points QQ and R,R, and also connect AA and B:B:
让我们将蓝色等边三角形的一侧延伸到新的点 QQ 和 R,R, 并连接 AA 和 B:B:

What must be true about the three yellow angles?
这三个黄色角必须是什么？

They are congruent. 它们是一致的。

They add to 180∘.180∘.
他们添加到 180∘.180∘.

They add to 360∘.360∘.
他们添加到 360∘.360∘.

Why is △QXZ△QXZ congruent to △RYZ?△RYZ?

SSScongruence
SSS全等

SAS congruence
SAS 全等

ASA congruence
ASA 全等

XZ‾XZ and YZ‾YZ are both parts of the equilateral triangle, so they are congruent.
XZ‾XZ 和 YZ‾YZ 都是等边三角形的一部分，因此它们是全等的。

One of the adjacent angles is 60∘+c.60∘+c.
其中一个相邻角是 60∘+c.60∘+c.

The other adjacent angle is 60∘.60∘.
另一个相邻角度是 60∘.60∘.

Therefore, we have a side and two adjacent angles congruent, making ASAASA congruence.
因此，我们有一条边和两个相邻的角全等，使 ASAASA 全等。 We know that △QXZ△QXZ is congruent to △RYZ.△RYZ. We also know the yellow angles are all congruent:
我们知道 △QXZ△QXZ 与 △RYZ.△RYZ. 全等我们也知道黄色角度都是全等的：

Geometric Stumpers 几何难题

All of the tools and techniques in this course are powerful. When you run into a hard problem that can’t be solved by one of your tools in one fell swoop, continue to look for ways to apply the strategies you know:
本课程中的所有工具和技术都非常强大。当您遇到一个无法用您的任何工具一举解决的难题时，请继续寻找应用您知道的策略的方法：

• Draw a diagram. 绘制图表。

• Find a pattern. 找到一个模式。

• Break the problem into parts.
  将问题分解成多个部分。

• Work backward. 逆向工作。

• Solve an easier but similar problem.
  解决一个更简单但类似的问题。

• Use a variable. 使用变量。

The next several problems will include challenging problems from a variety of geometry topics that provide good opportunities for employing these strategies.
接下来的几个问题将包括来自各种几何主题的具有挑战性的问题，这些问题为采用这些策略提供了很好的机会。

The next several problems will include challenging problems from a variety of geometry topics that provide good opportunities for employing these strategies.
接下来的几个问题将包括来自各种几何主题的具有挑战性的问题，这些问题为采用这些策略提供了很好的机会。

Which figure has more area shaded green?
哪个数字的绿色阴影区域更大？

A（✅）

B

A and B have the same area shaded green.
A 和 B 具有相同的区域，为绿色着色。

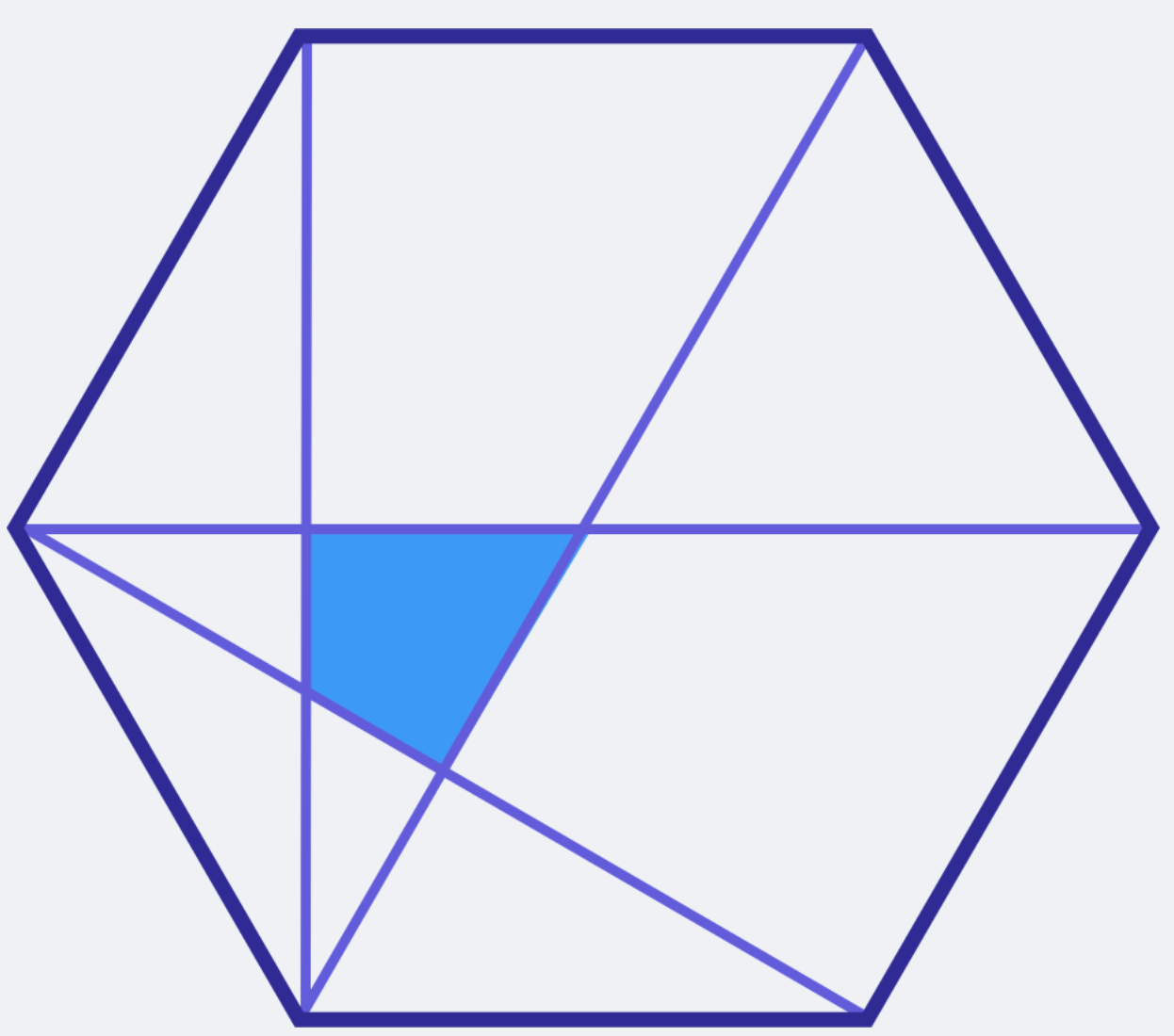
What is the area of the region shaded blue?
蓝色阴影区域的区域面积是多少？

Adding more lines of symmetry to the hexagon, we can split it into 3636 congruent triangles:
向六边形添加更多对称线，我们可以将其拆分为 3636 全等三角形：

Two of these triangles are shaded blue, so the area of the region shaded blue is
其中两个三角形为蓝色阴影，因此蓝色阴影的区域区域为

2/36=1/18

A cube with side lengths of 33 is painted and then sliced into unit cubes of side length 1:1:
绘制边长为 33 的立方体，然后将其切片为边长为 1:1: 的单位立方体

How many of the unit cubes have paint on at least two sides?
有多少个单位立方体的至少两个面上都有油漆？

16

18

19

20

22

If we look at the top layer of cubes, we see that 88 of the 99 will have at least two sides of paint on them:
如果我们查看立方体的顶层，我们会看到 99 的 88 上至少有两面的油漆：

Likewise, 88 of the unit cubes on the bottom layer will also have at least two sides of paint on them.
同样，底层的单位立方体的 88 也将至少有两面的油漆。

That leaves 44 cubes on the vertical edges that have not been counted that will also have two sides of paint on them.
这使得 44 立方体在垂直边缘上尚未计数，它们上也会有两面的油漆。

The total number of unit cubes with paint on at least two sides will be
至少两个面上有油漆的单位立方体的总数将为

8+8+4=20.8+8+4=20.

Is the amount of area shaded blue the same in each figure?
每个图中蓝色阴影的区域量是否相同？

Yes 是的

No 不

Explanation 解释

Each figure has a total area of 16.16.
每个图的总面积为 16.16.

FIgure A has two unshaded triangles, each with an area of 12(2)(4)=4,21​(2)(4)=4, so the shaded area is 16−4−4=8.16−4−4=8.
图 A 有两个无阴影的三角形，每个三角形的面积为 12(2)(4)=4,21​(2)(4)=4, ，因此阴影区域为 16−4−4=8.16−4−4=8.

Figure B has one shaded triangle with an area of 12(4)(4)=8.21​(4)(4)=8.
图 B 有一个面积为 12(4)(4)=8.21​(4)(4)=8. 的阴影三角形

Figure C has one shaded rectangle with an area of (2)(4)=8.(2)(4)=8.
图 C 有一个面积为 (2)(4)=8.(2)(4)=8. 的阴影矩形

Figure D has one shaded triangle with an area of 12(4)(3)=621​(4)(3)=6 and one shaded triangle with an area of 12(1)(3)=1.5.21​(1)(3)=1.5. The total shaded area in this figure is 6+1.5=7.5.6+1.5=7.5.
图 D 有一个面积为 12(4)(3)=621​(4)(3)=6 的阴影三角形和一个面积为 12(1)(3)=1.5.21​(1)(3)=1.5. 的阴影三角形，该图中的总阴影面积为 6+1.5=7.5.6+1.5=7.5.

Challenging Composites 具有挑战性的复合材料

Now that you’re warmed up for working with composite figures, let’s dive into some more complex examples. As we extend our work with composite figures to perimeters and surface areas as well, remember to apply the same strategies that worked well in the last lesson. In addition, look for shortcuts, or ways to group pieces of figures together.
现在，您已经为使用复合图形进行了热身，让我们深入研究一些更复杂的示例。当我们将复合图形的工作扩展到周长和曲面区域时，请记住应用在上一课中效果良好的相同策略。此外，寻找捷径或将图形片段组合在一起的方法。

How much total area is shaded yellow?

4π

7π

8π

11π

Transforming Tiles Part 1

变换瓦片第 1 部分

A tessellation fills the plane with regular polygons. A monohedral tiling fills the plane with congruent figures with no requirement that they’re regular polygons. In addition, vertices are allowed to touch at edges:
镶嵌使用规则多边形填充平面。 单面体平铺 用全等图形填充平面，无需它们是正多边形。此外，允许顶点在边处接触：

Note the rectangle tiling above has two types of vertices — one where 44 rectangles meet, and one where 33 rectangles meet.
请注意，上面的矩形平铺有两种类型的顶点 — 一种是 44 矩形相交的地方，另一种是 33 矩形相交的地方。

Two vertices are considered equivalent if the configuration of polygons touching one vertex is identical to that touching the other. How many distinct types of vertices are there in the tiling pattern shown?
如果接触一个顶点的多边形的配置与接触另一个顶点的多边形的配置相同，则认为两个顶点是等效的。显示的平铺模式中有多少种不同类型的折点？

Even complex-looking monohedral tiling can be based on simple shapes.
即使是看起来复杂的单面体平铺也可以基于简单的形状。

The pattern of dogs below is just based on transformations of a rectangle. You can take the portion inside the marked area and make a “dog stamp” that when repeated will make the picture:
下面的狗的模式只是基于矩形的变换。您可以取标记区域内的部分并制作一个 “狗印章” ，当重复时，它将形成图片：

The black-outlined figure was made by taking an equilateral triangle, cutting a smaller triangle with a point at the corner, and then rotating the cut portion until it went outside the original triangle. Will the black-outlined figure tessellate the plane?
黑色轮廓的图形是通过取一个等边三角形，切一个拐角处有点的小三角形，然后旋转切割部分直到它超出原来的三角形而制成的。黑色轮廓的图形会镶嵌飞机吗？

Yes 是的

No 不

One modification of a regular polygon that will still allow it to tile the plane is to cut a portion out and translate it between opposite sides. In this tiling, a triangle is cut from the right side of the square and moved to the left side of the square:
对规则多边形的一种修改仍然允许它平铺平面，即切出一部分并在相对的侧面之间平移。在此平铺中，从正方形的右侧剪切一个三角形，并将其移动到正方形的左侧：

Which figure below shows this operation performed twice?
下图哪个显示了此操作执行了两次？

(You may assume all sides that appear to be congruent are congruent.)
（您可以假设所有看起来全等的边都是全等的。

A

B

C

How many of these polygons will tile the plane?
这些多边形中有多少个将平铺平面？

(You may assume all sides that appear to be congruent are congruent, and rotation and reflection are allowed.)
（您可以假设所有看起来全等的边都是全等的，并且允许旋转和反射。

Only one of them will tile the plane.
其中只有一个会平铺平面。

Exactly two of them will tile the plane.
其中正好有两个会平铺这个平面。

Exactly three of them will tile the plane.
其中正好有三个会平铺平面。

All of them will tile the plane.
所有这些都将平铺平面。

A. Translate the cut triangle:
A. 平移剪切的三角形：

B. Rotate and translate the cut triangle:
B. 旋转并平移剪切的三角形：

C. Reflect and translate the cut triangle:
C. 反射并平移剪切的三角形：

Each of the three tiles A, B, and C is made by cutting a triangle from the first shape above them and placing it on another portion of the shape. Which one will not tessellate?
三个图块 A、B 和 C 中的每一个都是通过从它们上方的第一个形状切出一个三角形并将其放置在形状的另一部分来制成的。哪一个不会 镶嵌？

A

B

C

Transforming Tiles Part 2

The type of transformation done can affect the placement of the overall pattern.

In the lizard pattern above, after a lizard is placed there’s a translation and 120∘120∘ rotation, linking the lizards in a triangle:

The shapes given are solid — the lines are added as a guide:

Suppose you tiled using one of the shapes above so that the “notch” from the previous shape fits into the next one via applying reflection and translation to the right to the whole shape (no up or down movement allowed). Which piece will work?

A

B

C

None of the above

假设您使用上面的形状之一进行平铺，以便通过对整个形状右侧应用反射和平移（不允许向上或向下移动），使前一个形状的“缺口”适合下一个形状。哪件作品会奏效？

A

B

C

None of the above 以上都不是

Explanation 解释

For the two (A and C) that don’t work, when reflecting and fitting the “notch,” there’s some up-and-down movement. This doesn’t occur with reflections of B (shown below):
对于不起作用的两个（A 和 C），当反射和拟合 “缺口” 时，会有一些上下运动。B 的反射不会发生这种情况 （如下所示）：

The shape given is solid, and the lines are added as a guide:
给出的形状是实心的，并添加线条作为参考线：

Only performing the transformations in vertical or horizontal directions, what transformations are necessary to make this pattern?
只执行垂直或水平方向的变换，需要哪些变换才能形成这个 pattern？

Translation only 仅翻译

Translation and reflection only
仅平移和反射

Translation and rotation only
仅平移和旋转

Translation, rotation, and reflection
平移、旋转和反射

Explanation 解释

For the pieces to fit, each one needs to be both rotated and reflected from the previous.
为了使这些部分适合，每个部分都需要旋转并从前一个部分反映出来。 Which of the above polygons will tile the infinite plane?

(You may assume all sides that appear to be congruent are congruent, and reflections and rotations are allowed.)

Only A

Only B

Both A and B

Neither A nor B

Why?

Explanation

A won’t tile the plane:

Note that, by fitting the notches, there’ll be a hexagon on the inside of the pattern which will be unable to be tiled.

B will tile the plane:

Note that each alternating “stripe” of hexes is a reflection of the one adjacent.

Which of the above polygons will tile the infinite plane?

(You may assume all sides that appear to be congruent are congruent.)

Only A

Only B

Both A and B

Neither A nor B # Irregular Tiles 不规则瓦片

Not all tessellations are based on regular polygons or transformations of regular polygons. This lesson will focus on monohedral tiling — filling the plane with repetitions of the same congruent shape — with irregular polygons.
并非所有分割都基于常规多边形或常规多边形的转换。本课将重点介绍单面体平铺 — 用不规则多边形填充相同全等形状的重复项来填充平面。

The tetromino and pentomino below are solid shapes — the lines are given as guides. Which will tile the infinite plane?
下面的四联骨牌和五联骨牌是实心形状 —— 线条作为参考线给出。哪个会平铺无限平面？

A

B

Both A and B
A 和 B

Neither A nor B
既不是 A 也不是 B Explanation 解释

Both A and B tile the infinite plane, as shown below:
A 和 B 都会 平铺无限平面，如下所示：

Is it possible to make a triangle that cannot tile the infinite plane?
是否可以制作一个 不能 平铺无限平面的三角形？

Yes 是的

No 不

Explanation 解释

Any two congruent triangles can be fit together to make a parallelogram, as shown:
任意两个全等三角形可以拟合在一起形成平行四边形，如下所示：

Then the parallelograms can make a tessellation, as shown:
然后平行四边形可以进行镶嵌，如下所示：

Which of the quadrilaterals above tile the infinite plane?
上面的哪个四边形平铺了无限平面？

A only 仅

B only  仅限 B

Both A and B
A 和 B

Neither A nor B
既不是 A 也不是 B Explanation 解释

A general procedure for tiling any quadrilateral is to tile copies with a version rotated 180180 degrees as in the examples shown here:
平铺任何四边形的一般过程是使用旋转 180180 度的版本平铺副本，如下所示：

Which of the pentagons above tile the infinite plane? Note that the vertices don’t need to touch.
上面的哪个五边形平铺了无限平面？请注意，顶点不需要接触。

A only 仅

B only  仅限 B

Both A and B
A 和 B

Neither A nor B
既不是 A 也不是 B

Explanation 解释

Three copies of A can form a hexagon, as shown:
A 的三个副本 可以形成一个六边形，如下所示：

We already saw from a previous lesson that because 360/108360/108 doesn’t divide without remainder, there’s no regular tiling with a pentagon. Unfortunately, even when allowing the pentagon to be arranged touching a side, that would only allow for 180∘180∘ angles. Since
我们已经在上一节课中看到，因为 360/108360/108 不会在没有余数的情况下进行除法，所以没有带有五边形的规则平铺。不幸的是，即使允许五边形接触一侧，也只允许 180∘180∘ 角度。因为

360∘−180∘−108∘=72∘,360∘−180∘−108∘=72∘,

there’s no way to fit an extra pentagon:
没有办法容纳额外的五边形：

When taking convex pentagons in general (like from the last question), there are 1515 known varieties that tile the plane, and only recently ((July 2017)2017) has it been proven that every variety is accounted for. This pentagon tiling was discovered in 2015:2015:
当一般采用凸五边形时（就像上一个问题一样），有 1515 已知的变体可以平铺平面，直到最近 (( July 2017)2017) 才证明每个变体都被考虑在内。这个五边形平铺是在 2015:2015: 中发现的

The four shapes above are called heptiamonds and made by adjoining seven congruent equilateral triangles. One of the shapes cannot tile the plane. Which one?
上面的四个形状称为 heptiamonds ，由七个全等三角形相邻而成。其中一个形状 无法 平铺平面。哪一个？

Note that each shape is continuous — the lines are included as a guide.
请注意，每个形状都是连续的 - 线条作为参考线包含在内。

A

B

C

D The four shapes above are called heptiamonds and made by adjoining seven congruent equilateral triangles. One of the shapes cannot tile the plane. Which one?
上面的四个形状称为 heptiamonds ，由七个全等三角形相邻而成。其中一个形状 无法 平铺平面。哪一个？

Note that each shape is continuous — the lines are included as a guide.
请注意，每个形状都是连续的 - 线条作为参考线包含在内。

A

B

C

D

Explanation 解释

The possible tilings of A, B, and D are shown here:
A、B 和 D 的可能平铺 如下所示：

For shape C, adjoining two copies must be done like the one shown on the left (with possible reflection) below. Doing so puts a two-triangle gap that cannot be filled without overlap (see the attempt using the blue copy of the shape):
对于形状 C，必须像下面左侧所示（可能有反射）那样完成两个相邻的副本。这样做会留下一个两个三角形的间隙，如果不重叠就无法填充（请参阅使用形状的蓝色副本的尝试）：

True or False? 对还是错？

Every convex pentagon with two parallel sides (like the one shown above) can be used to make a monohedral tiling.
每个具有两个平行边的凸五边形（如上所示）都可用于制作单面体平铺。

True 真

False 假

Explanation 解释

Here’s a general procedure:
下面是一般过程：

1. Rotate the pentagon 180∘180∘ and adjoin the ends. This forms a hexagon.
   旋转五边形 180∘180∘ 并连接两端。这形成了一个六边形。

2. Iterate the hexagons side by side with the parallel sides touching.
   并排迭代六边形，平行边接触。

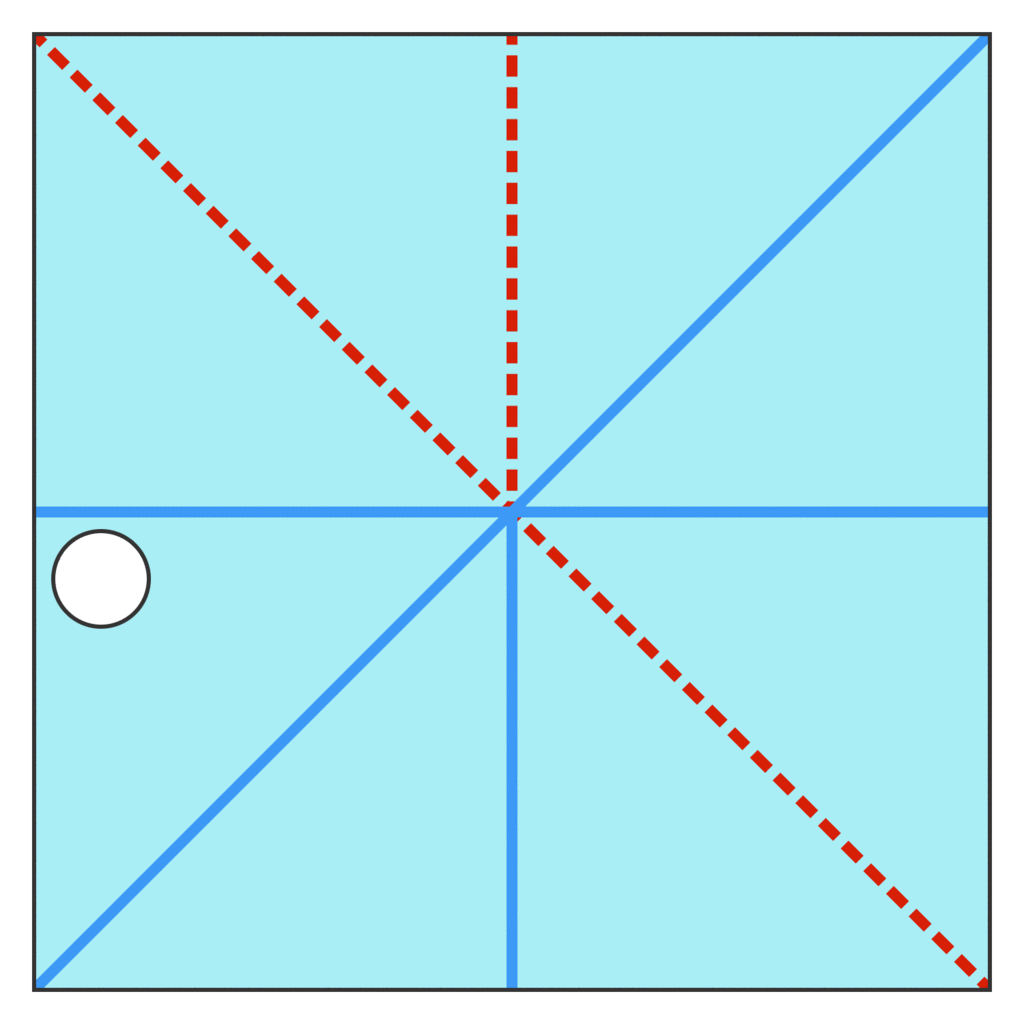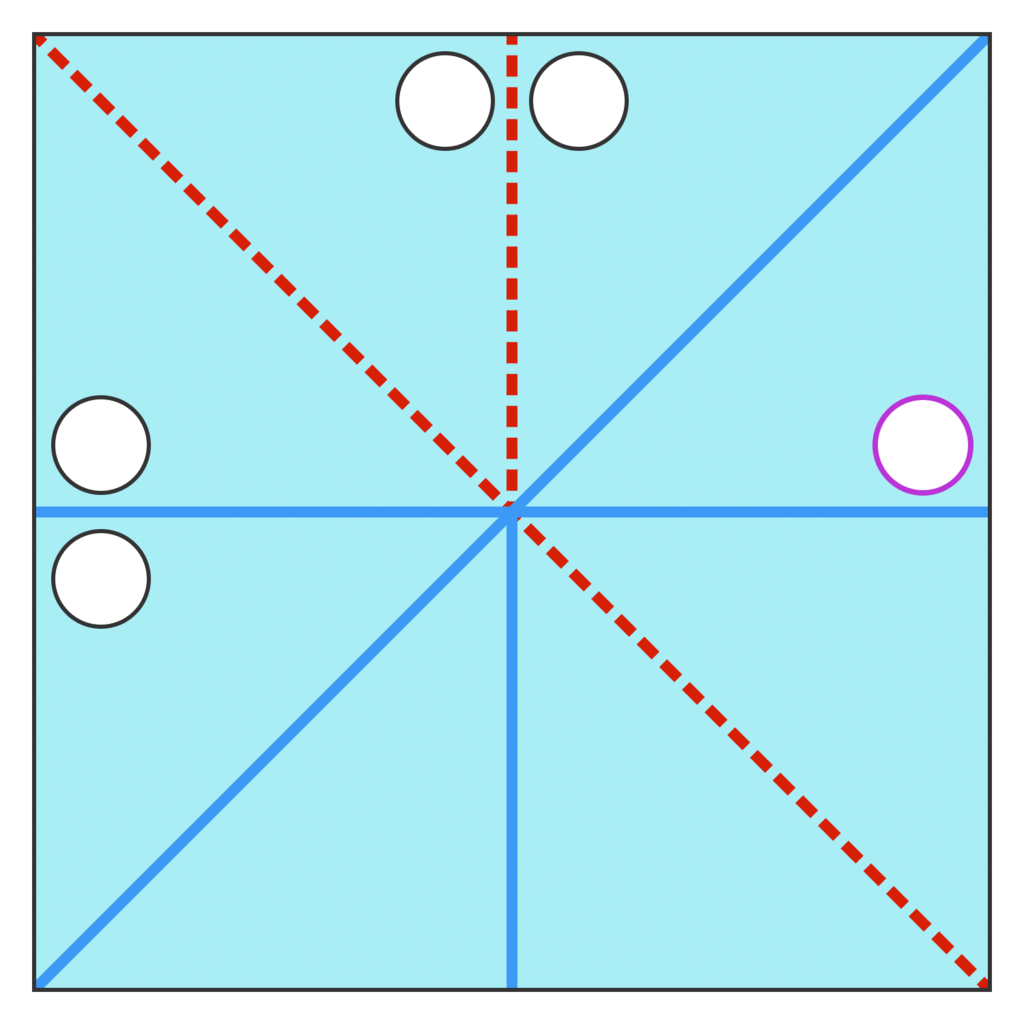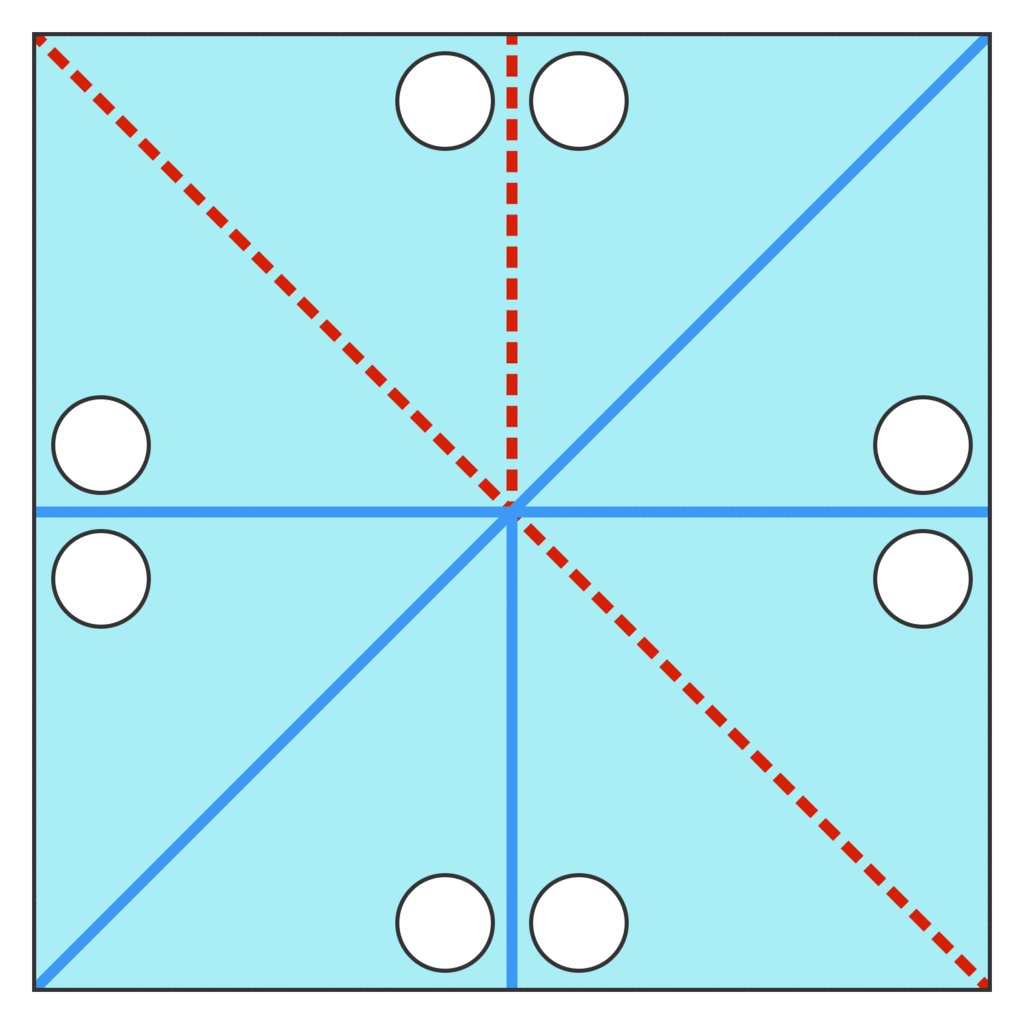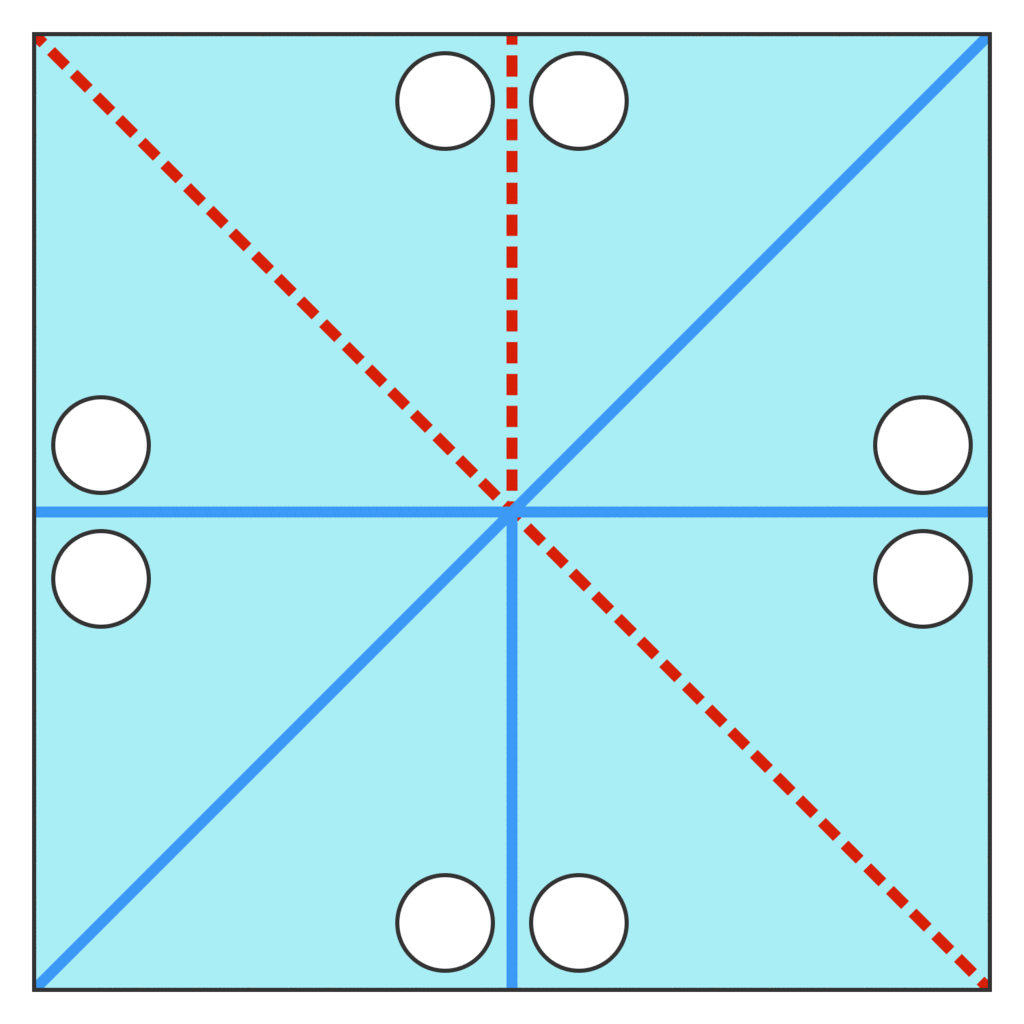
Guards in the Gallery 画廊中的守卫

The irregular purple polygon above, made of five
上面的不规则紫色多边形，由 5 个congruent 全等 squares, is the floor plan of an art gallery.
squares，是艺术画廊的平面图。

Your job is to position some number of unmoving guards — who cannot see through walls — so that every location in the gallery is in view of at least one of the guards. It’s possible, as shown in the example, to guard this particular museum with two guards:
你的工作是安置一些一动不动的守卫 - 他们无法透过墙壁看到 - 这样画廊中的每个位置都至少有一个守卫可以看到。如示例中所示，可以使用两个守卫守卫这个特定的博物馆：

Is it possible to guard this entire gallery with only one guard?
有没有可能只用一个守卫守卫整个画廊？

Yes 是的

No 不

Explanation 解释

Consider the two places marked with stars. A guard has to be standing on the orange region to see the star on the left, and a guard has to be standing on the green region to see the star on the right. Since the two regions don’t intersect, one guard is insufficient to guard the gallery.
考虑标有星星的两个地方。必须有一名警卫站在橙色区域才能看到左边的星星，必须有一名警卫站在绿色区域才能看到右边的星星。由于这两个区域不相交，因此一个守卫不足以保护通道。

Using the same rules as before, what’s the fewest number of guards needed to guard this gallery?
使用和以前一样的规则， 守卫这个画廊所需的最少守卫数量是多少？

33

44

55

66

Explanation 解释

A possible placement with four guards is shown above — the entire gallery is then visible.
上面显示了一个可能的位置，其中有四个守卫 —— 然后可以看到整个画廊。

We’re going to prove four is necessary by picking four specific spots within the gallery that must all be seen — since the entire gallery must be visible: (These don’t represent where guards are placed, these represent a selection of spots the guards must see.)
我们将通过在画廊中挑选四个必须全部看到的特定位置来证明四个是必要的——因为整个画廊都必须可见：（这些不代表警卫的位置，这些代表警卫必须看到的一系列位置。

The four stars above marked red, orange, green, and blue must all be seen by at least one guard, but none of the regions where a guard needs to stand to see a particular star intersect. This means for any one guard they can only see at most one star. Therefore, a three-guard solution is impossible.
上面标记为红色、橙色、绿色和蓝色的四颗星星都必须被至少一名警卫看到，但警卫需要站着才能看到特定星星的任何区域都没有相交。这意味着对于任何一个守卫来说，他们最多只能看到一颗星星。因此，三守解决方案是不可能的。

This particular gallery is a little more irregular and isn’t just a set of squares joined together.
这个特殊的画廊有点不规则，而不仅仅是一组连接在一起的方块。

Using the same rules as before, what’s the fewest number of guards needed to guard this gallery?
使用和以前一样的规则， 守卫这个画廊所需的最少守卫数量是多少？

11

22

33

44

Explanation 解释

The left image shows a solution with two guards, so at least one of the two guards has line of sight to every position in the gallery:
左图显示了一个具有两个 guard 的解决方案，因此两个 guard 中至少有一个可以看到画廊中的每个位置：

Why are at least two guards necessary?

The positions marked with a cake and a donut must be visible to at least one guard. (They are not places guards will be placed, they are places the guards must see.)
标有蛋糕和甜甜圈的位置必须至少有一名警卫可以看到。（他们是 不是警卫会被安置的地方，而是警卫必须看到的地方。

The cake is visible to any guard in the red region, and the donut is visible to any guard in the green region.
蛋糕对红色区域的任何守卫都可见，而甜甜圈对绿色区域的任何守卫可见。

Since the two regions don’t overlap, there’s no place for a guard to stand to see both at the same time. So the gallery can’t be guarded by just one guard.
由于这两个区域不重叠，因此没有地方让警卫站着同时看到这两个区域。所以画廊不能只由一名警卫守卫。

Using the same rules as before, what’s the fewest number of guards needed to guard this gallery?
使用和以前一样的规则， 守卫这个画廊所需的最少守卫数量是多少？

11

22

33

44

55

Explanation 解释

The diagram can be reduced to simple shapes like this:
该图可以简化为简单的形状，如下所示：

If one guard is placed at the intersection of the blue polygons and another guard is placed at the intersection of the red polygons, the entire museum is guarded.
如果一个守卫放置在蓝色多边形的交集处，另一个守卫放置在红色多边形的交集处，则整个博物馆都处于守卫状态。

To see that one guard won’t be enough, note that there’s no place to stand so the two marked points below are both visible:
要看到一个守卫是不够的，请注意没有地方可以站立，因此下面的两个标记点都可见：

One last problem, and the trickiest of the set!

What’s the fewest number of guards needed for this gallery?

(You can assume any region of the gallery that appears to be a rectangle is, in fact, a rectangle.)

3✅ Explanation

The diagram above shows a more abstract version of the map, with the shapes reduced to (mostly) rectangles. One guard at each star point guards all of the areas marked with the same color, so 33 guards are sufficient.

To see that it won’t work with two guards, notice in the diagram below that there’s no location that can see any 22 of the 33 black stars at the same time. That means at least 33 guards are needed to see all 33 stars:

You might start to suspect there’s a systematic way to solve this kind of problems, and there is:
您可能开始怀疑有一种系统的方法来解决此类问题，并且有：

As part of the course, we’ll teach a truly wonderous coloring proof for finding the fewest number of guards needed for this kind of puzzle, and look at some twists like “internal walls” and “worst-case scenarios”:
作为课程的一部分，我们将教授一个真正精彩的 着色证明 ，以找到此类谜题所需的最少数量的守卫，并研究一些曲折，如 “内墙” 和 “最坏情况”：

Proceed onward to learn some beautiful geometry.
继续学习一些漂亮的几何学。

Polyomino Tiling 聚联骨牌平铺

These puzzles all involve polyominoes, shapes constructed by attaching two or more congruent squares side by side:
这些谜题都涉及 多联骨牌，即通过并排连接两个或多个全等正方形来构建的形状：

The shape above is a pentomino because it uses 55 squares, but any number of squares is possible. In the puzzles ahead, you’ll fit them together into shapes and patterns like this tesselation:
上面的形状是五联骨牌，因为它使用 55 个方块，但任意数量的方块都是可能的。在前面的拼图中，您将将它们组合在一起，形成形状和图案，如以下镶嵌：

Using only copies of the polyomino on the left (rotations allowed), is it possible to fill the shape on the right without overlapping or gaps?
仅使用左侧的多联骨牌副本（允许旋转），是否可以填充右侧的形状而不会重叠或间隙？

Yes 是的

No 不

Explanation 解释

The shape can be filled with five copies of the polymino.
形状可以用 5 个 polymino 副本填充。

The type of puzzle you just did is called a tiling. To be considered a tiling, the polyominos need to cover the entire shape without any gaps or overlaps.
您刚才做的拼图类型称为 平铺。要被视为平铺，多联骨牌需要覆盖整个形状，没有任何间隙或重叠。

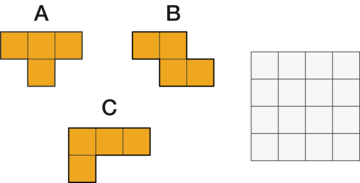
If one of the squares marked with a letter is removed, the shape on the right can be tiled by the polyomino on the left. Which square should be removed?
如果删除了其中一个标有字母的方块，则右侧的形状可以被左侧的多联骨牌平铺。应该删除哪个方格？

A

B

C

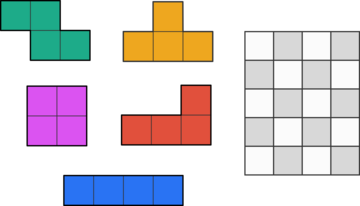
For two of the three tetrominoes on the left, it’s possible to use 44 copies of that tetromino (with rotation allowed) to tile a 4×44×4 square.
对于左侧三个四极骨中的两个，可以使用该四极骨的 44 副本（允许旋转）来平铺 4×44×4 方块。

One of the tetrominoes will not be able to tile the square. Which one?
其中一个四极骨牌将无法 平铺方格。哪一个？

A

B

C

If I have the five colored shapes shown that I can rotate, and I use each shape once, is it possible to place them so they fit perfectly in a 5×45×4 rectangle?
如果我显示了可以旋转的五个彩色形状，并且每个形状使用一次，是否可以放置它们以使其完美地适合 5×45×4 矩形？

(The checkerboard pattern is a hint.)
（棋盘格图案是一个提示。

Yes 是的

No 不

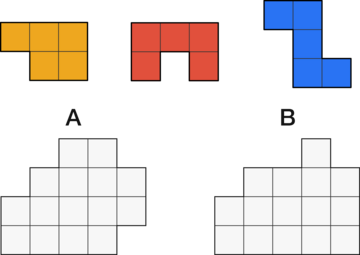
The three pentominoes on top can be used to tile one or both of the larger shapes. Which one(s)?
顶部的三个五联骨牌可用于平铺一个或两个较大的形状。哪一个（s）？

(Pieces can be rotated or reflected, and all three pentominoes must be used on a given tiling.)
（块可以旋转或反射，并且 所有三个 五联骨牌都必须在给定的平铺上使用。

A only 仅

B only  仅限 B

Both A and B
A 和 B

Neither A nor B
既不是 A 也不是 B

Explanation 解释

The solution for B is below:
B 的解 如下：

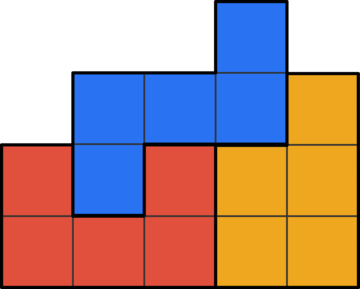
For A, the upper-right corner only can work with the yellow shape, but the remaining two pieces won’t fit in either case:
对于 A，右上角只能与黄色形状一起使用，但其余两个部分在任何一种情况下都不适合：

Mathematical Origami 数学折纸

In the next several lessons, we’ll explore some profound mathematics that relates to origami — paper folding. However, to be clear, we won’t talk much at all about folding animals or complex projects in these lessons. Instead, we’ll be focusing on some geometric questions that you can ask about how paper can be folded and about the physical results of different folding instructions:
在接下来的几节课中，我们将探索一些与折纸——纸张折叠——相关的深刻数学知识。然而，为了明确起见，在这些课程中我们不会过多讨论折叠动物或复杂的项目。相反，我们将专注于一些关于如何折叠纸张以及不同折叠指令产生的物理结果的几何问题。

So, prepare yourself to think logically and creatively to figure out these paper folding challenges.
因此，请准备好逻辑地和创造性地思考，以解决这些纸张折叠难题。

What’s mathematical about origami?
折纸有什么数学性质？

• Folding instructions are like an algorithm for making a certain shape. Even extremely complex projects can be broken down to simple steps of only a few different types — fold a portion of the paper up or down, tuck in a corner, etc.
  折叠说明就像制作特定形状的算法。即使是极其复杂的项目，也可以分解为仅几种不同类型的简单步骤——向上或向下折叠纸的一部分，将一角藏进去等。

• Using the alignment of the edges and previously made creases in the paper, it’s possible to fold a piece of paper very precisely. Folding a paper in half or into fourths, for example, is pretty easy, but how about folding it precisely into thirds? Figuring out how to make extremely precise folds is definitely a mathematical task.
  利用纸张边缘的对齐以及先前制作的折痕，可以非常精确地折叠一张纸。例如，将纸张对折或四等分相当容易，但如何精确地将其折叠成三等分呢？确定如何制作极其精确的折叠绝对是一项数学任务。

• Paper is a flat plane, and if you can’t tear or cut it, then there are limits to what shapes it can be folded into. Sometimes the final shape desired is flat, sometimes it might be a 3D3D figure that holds its shape because of how the paper bends in space.
  纸是一种平面，如果无法撕裂或切割它，那么它能折叠成的形状是有局限的。有时最终想要的形状是平坦的，有时它可能是一个 3D3D 图形，因为它在空间中弯曲的特性保持了形状。

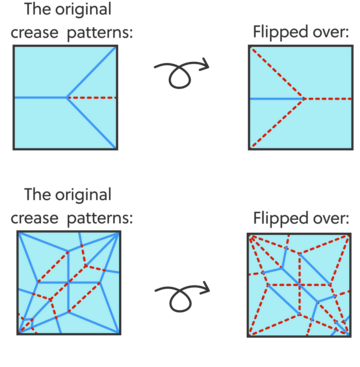
The geometric design on the far right below is the result of folding and unfolding a simple paper crane. It’s the pattern of all of the creases made in the paper when the crane is folded, and it’s called the mountain-valley pattern for the crane:
下方最右边的几何设计是折叠和展开一张简单纸鹤的结果。它是纸鹤折叠时所做所有折痕的模式，被称为纸鹤的山谷模式：

In the final crane, the four corners of the paper become
在最后一架起重机中，纸张的四个角变成了

1. the tip of the left wing,
   左翼的尖端

2. the tip of the right wing,
   右翼的尖端

3. the tip of the tail, and
   尾巴的尖端，和

4. the crane’s head. 起重机的头。

Using your intuition for the crane’s symmetry, which corner of the mountain-valley pattern was the crane’s head before the paper was unfolded?
利用你对鹤的对称性的直觉，在纸张展开之前，鹤的头部位于山谷图案的哪个角落？

Top left 左上角

Top right 右上角

Bottom left 左下角

Bottom right 右下角

Explanation 解释

Look at the two pairs of opposite corners of the mountain-valley pattern:
观察山川图案中的两组相对角：

The top-left and bottom-right corners are symmetric, whereas the top-right and bottom-left corners are not. Therefore, the top-left and bottom-right corners must be the two wings, and the top-right and bottom-left corners must be the head and tail.
顶部左上和底部右下角是对称的，而顶部右上和底部左下角则不是。因此，顶部左上和底部右下角必须是两个翼部，而顶部右上和底部左下角必须是头部和尾部。

Comparing the top-right corner to the bottom-left corner, notice that the bottom-left corner has one additional zig-zag crease. This is the crease made by folding down the head. Therefore, the bottom-left corner must be the corner which became the head of the swan.
比较右上角和左下角，可以注意到左下角多了一个锯齿状的折痕。这是折叠头部时形成的折痕。因此，左下角必须是成为天鹅头部的那个角。

An extra remark: 额外说明：

If you make your own crane, your mountain-valley pattern might look more complex.
如果你自己制作起重机，你的山谷模式可能会看起来更复杂。

If you try making your own origami crane and you unfold the paper after the crane is complete, you’ll likely find that there are extra creases in your paper that aren’t in the diagram in this problem. This is because most crane-folding instructions will cause you to create “guide creases” that are used to indicate where future creases need to go, but are actually not kept as folds in the final crane. The diagram in this problem is of only true creases — creases that remain in the final, folded crane.
如果你自己尝试折纸鹤，然后在完成纸鹤后展开纸张，你很可能会发现纸张上有额外的折痕，这些折痕不在这个问题中的图纸上。这是因为大多数折纸鹤的指示通常会让你创建“指导折痕”，用于指示未来需要去哪里的折痕，但实际上这些折痕不会保留在最终的纸鹤中。这个问题中的图纸只显示了真正的折痕——留在最终折叠纸鹤上的折痕。

Mountain and Valley Creases:
山川褶皱：

When we unfold an origami project, we can see both where all of the creases were and which way the paper was bent at each crease. When the paper is creased so that the crease is on the outside/top, we call it a mountain crease. When the paper is creased so that the crease is on the inside/bottom, we call it a valley crease. This is where the mountain-valley pattern gets its name — it’s the record of where the creases are and whether each one is a mountain crease or a valley crease:
当我们展开一个折纸项目时，我们可以看到所有折痕的位置以及每个折痕处纸张的弯曲方向。当折痕使折痕位于外部/顶部时，我们称之为山形折痕。当折痕使折痕位于内部/底部时，我们称之为山谷折痕。这就是山谷模式命名的原因——它是记录折痕位置以及每个折痕是山形折痕还是山谷折痕的记录。

Note that when we flip a crease pattern over, all of the mountains become valleys and all of the valleys become mountains:
注意，当我们翻转折痕模式时，所有的山峰都会变成山谷，所有的山谷都会变成山峰：

Now consider this folding:
现在考虑这个折叠：

• Fold 1:1: We fold a square piece of paper in half to make a rectangle. Since it’s a valley fold, the back of the paper becomes the outside and the front is on the inside.
  我们将一张正方形的纸对折，得到一个矩形。因为是山谷折，所以纸的背面在外面，正面在里面。

• Fold 2:2: We fold it in half again with another valley fold to make a small square.
  我们将它再次对折，再用山谷折法折成一个小正方形。

• Lastly, we unfold the paper entirely.
  最后，我们将纸张完全展开。

Which of these might be the mountain-valley pattern we see after executing the instructions above?
这些中哪一个可能是执行了上面的指令后我们看到的山谷模式？

A

B

C

Above, we fold a square piece of paper twice in succession, and then fully unfold it. What’s the resulting mountain-valley pattern?
以上，我们连续对一张正方形的纸张对折两次，然后完全展开它。最终的山谷图案是什么样的？

A

B

When we fold a paper many times before unfolding it, the geometry of the mountain-valley pattern can get quite complicated, as can the patterns which describe which creases are mountains and which are valleys. Both of these effects happen when paper is folded at least twice in succession.
当我们多次折叠纸张然后再展开它，山谷图案的几何形状会变得相当复杂，描述哪些折痕是山峰，哪些是山谷的模式也是如此。这两种效果都会在纸张连续折叠至少两次时发生。

Joint Mountain+Valley Creases:
联合山+谷褶皱:

When an area of paper is folded twice or more in succession, the first fold through the area might be a straight line and will result in a mountain or valley crease all the way across the paper. However, the second fold is made after the paper is already folded over itself. So, the top layer is folded on a line and with an orientation — mountain or valley — that is “symmetric but opposite” to how the bottom layer is being folded.
当纸张区域连续折叠两次或更多次时，第一次折叠可能是一条直线，并会在整张纸上形成一座山或山谷折痕。然而，第二次折叠是在纸张已经折叠在自己身上的情况下进行的。因此，顶层在一条线上折叠，并以与底层“对称但相反”的方式折叠，即山折或山谷折。

Symmetrically “Bent” Creases:
对称地“弯曲”的折痕：

There are also many intersections where there’s one straight-looking crease and another crease symmetrically “bent” where it intersects the first.
也有很多交叉点，其中一个看起来是直线的折痕，而另一个折痕在交点处对称地“弯曲”。

Here, we fold three times and then fully unfold:
在这里，我们折叠三次，然后完全展开：

• Fold 1:1: Fold the square in half with a mountain fold to make a tall rectangle.
  折叠 1:1: 将正方形对折成山形折痕，形成一个长方形。

• Fold 2:2: Fold the top half of the rectangle down with a valley fold to make a small square.
  折叠 2:2: 将矩形的上半部分向内进行山谷折叠，形成一个小正方形。

• Fold 3:3: Fold that small square along the diagonal with a valley fold to make a right triangle.
  折叠 3:3: 将那个小正方形对角线处进行山谷折叠，形成一个直角三角形。

• Lastly, entirely unfold the paper.
  最后，完全展开这张纸。

Which of these four mountain-valley patterns would be made by executing the above steps?
这四个山谷模式中的哪一个将由上述步骤执行产生？

S

T

U

V

The mountain-valley patterns below were each made by first valley-folding a square along the horizontal diagonal:
下方的山谷模式都是首先沿水平对角线折叠正方形形成的

Suppose we’re given these patterns:
假设我们得到了这些模式：

Which mountain-valley pattern corresponds to the instructions above where the 22ndnd step is “tuck the right-corner flap inside so that we can’t see it from the front or back anymore”?
哪座山谷模式与上述指令对应，其中 22 ndnd 步骤是“将右角折片藏在里面，这样从前或背后就看不见了”？

A

B

C

D

Marcus completely unfolds four sheets to look at their mountain-valley patterns. Which mountain-valley pattern must have been made following different folding instructions than the instructions used to make the other three?
马库斯完全展开四张纸，观察它们的山谷图案。哪个山谷图案可能是按照与制作其他三张纸不同的折叠指示制作的？

Note: The sheets may have been rotated or flipped since they were first folded.
注意：这些纸张可能在最初折叠后被旋转或颠倒了。

H

I

J

K

The next several lessons investigate the patterns created by folding long strips of paper in several places. Here’s an example:
接下来的几节课将探讨通过在纸张的多个位置折叠长条形纸张所创建的模式。以下是一个例子：

The piece of paper above is a rectangle that’s 50 cm50 cm long when unfolded. If it’s folded on the creases shown, approximately how long will the resulting rectangle be?
这张纸张展开时的长度是 50 cm50 cm 。如果按照所示的折痕折叠，得到的矩形大约会有多长？

20 cm20 cm

35 cm35 cm

40 cm40 cm

45 cm45 cm

Explanation 解释

If the paper is folded as shown, the strip will fold up as a zig-zag:
如果将纸张按照所示的方式折叠，条状物将折叠成锯齿状：

The third picture above is of the folded paper strip as seen from the side. You can ignore the length of the red and blue parts connecting the three segments (they indicate where the creases are made), but when the paper is folded flat, they are effectively just three flat layers zig-zagging back and forth.
上面的第三张图片是从侧面看到的折纸条。可以忽略连接三段的红蓝部分的长度（它们表示折痕的位置），但在纸张被折叠成平面时，它们实际上只是三个平铺的层来回曲折。

Solution 1:1: Starting from the left, the zig-zag moves toward the right for 15 cm,15 cm, then back left for 5 cm,5 cm, and then toward the right again for 30 cm.30 cm. Therefore, the total length of the folded paper is 15−5+30=4015−5+30=40 centimeters.
解决方案 1:1: 从左开始，折线向右移动 15 cm,15 cm, 然后向左移动 5 cm,5 cm, 再次向右移动 30 cm.30 cm. 因此，折叠纸张的总长度是 15−5+30=4015−5+30=40 厘米。

Solution 2:2: In the middle of the zig-zag, the paper is three layers thick, and everywhere else it’s one layer thick. Imagine cutting up the paper and removing the extra layers where the pieces overlap. In total, 2×5=102×5=10 centimeters of paper would be removed, and the remaining single layer would be 50−10=4050−10=40 centimeters long.
解决方案 2:2: 在曲折的中间部分，纸张是三层厚，其他地方则是单层。想象将纸张切割并移除重叠部分的多余层。总共 2×5=102×5=10 厘米的纸张会被移除，剩余的单层纸张长度为 50−10=4050−10=40 厘米。

Dragon Folding

Suppose you take a strip of paper and valley-fold it in half so the left end meets the right end, and then you valley-fold the folded strip in half so its left end meets its right end, as shown above.

A.

B.

C.

D.

If you completely unfold the strip by reversing the actions, what will the mountain-valley pattern look like?

A

B

C

D

Why?

If you take a strip of paper and valley-fold it in half so the left end meets the right end three times, as shown above, then the crease pattern evolves as follows:

If you take the thrice-folded strip and again valley-fold it in half so the right end meets the left end, and then unfold the entire strip, how many mountain and valley creases will there be on the unfolded strip?

66 mountain creases, 77 valley creases

77 mountain creases, 66 valley creases

77 mountain creases, 88 valley creases

88 mountain creases, 77 valley creases

Why?

If you take a strip of paper and valley-fold it in half so the left end meets the right end three times, as shown above, then the crease pattern evolves as follows:

The crease in the first position from the left after the second fold is a mountain crease. This crease is in the second position after the third fold.

If you valley-fold the thrice-folded paper in half twice more (so it has been valley-folded in half five times total), what will be the position of the mountain crease described above?

44

55

66

77

88

Why? If you take a strip of paper and valley-fold it in half so the left end meets the right end five times, and then unfold the entire strip, will the 66thth crease from the left be a mountain crease or a valley crease?

Mountain

Valley

Why? Suppose we valley-fold the strip of paper in half 100100 times. Will the 6th6th crease from the left be a mountain crease or a valley crease?

Mountain

Valley

Why?

If we valley-fold the paper in half 100100 times, and then unfold the strip and observe the crease pattern, how long will the longest run of consecutive valley creases be?

22

33

99

100100

Why?

If, when unfolding the paper, you only unfold the creases to right angles rather than all the way flat, you get an interesting sequence of shapes:

Each of these shapes is a dragon curve. The reason for this name becomes more apparent as the number of valley folds increases:

Note: In these images, we’re zooming in by a factor of 22 each time, so the length of a region appears to stay the same even though in fact the length of a region is halved with each valley fold.

2D Holes and Cuts 二维孔和切口

If we mountain-fold a square piece of paper in half twice and then punch a hole all the way through the multiple layers of the folded paper, as shown above, how many holes will there be when we unfold the paper?
如果我们将一张正方形纸张对折两次，然后穿透多层折叠的纸张打一个孔，如上图所示，当我们展开纸张时，会有多少个孔？

11

22

44

88

Explanation 解释

After the two folds, there will be four square layers of paper, each exactly coinciding with the others. Thus, when we punch the hole through the folded paper, we’ll punch a hole through each of these four layers — when we unfold the paper, there will be four holes, one in each layer.
经过两次折叠，会有四层正方形的纸张，每层都完全重合。因此，当我们穿透折叠的纸张打孔时，会在这四层上都打一个孔——当我们展开纸张时，会有四个孔，分别在每一层上。

If we mountain-fold a square piece of paper in half twice and then punch a hole all the way through the multiple layers of folded paper, as shown in the animation above, where will the holes be when we unfold the paper?
如果我们将一张正方形纸张对折两次，然后穿透多层折叠的纸张打一个洞，如上图动画所示，当我们展开纸张时，洞会在哪里？

A

B

C

D

Explanation 解释

To help see what’s going on, let’s label the four regions the folding divides the paper into.
为了帮助理解情况，让我们给折叠将纸张分为的四个区域标上标签。

Let’s start with Region 1.1. Both mountain folds leave it fixed in place, so when the hole is punched through the folded paper, Region 11 is in the same position it will be in when the paper is unfolded. Thus, since the hole goes through the top-left corner of each layer (when folded), this hole will appear in the top-left corner of Region 11 when the paper is unfolded, as shown above.
让我们从区域 1.1. 开始。两个山形折叠使其固定在原位，因此在穿过折叠纸张的孔时，区域 11 的位置与纸张展开后的位置相同。因此，由于孔穿过每层的左上角（折叠时），这个孔在纸张展开后将出现在区域 11 的左上角，如上图所示。

Next, let’s look at Region 2.2. The first mountain fold “reflects” Region 22 across its bottom edge, and the second mountain fold leaves this reflection fixed in place. Thus, the top-left corner of Region 22 when the hole is punched will be the bottom-left corner when the paper is unfolded.
接下来，我们来看区域 2.2. 。第一个山形折痕“映射”了区域 22 的底部边缘，而第二个山形折痕保持这个映射不变。因此，当在纸张上打孔时，区域 22 的左上角位置，展开后会成为左下角位置。

The first mountain fold reflects Region 33 across its bottom edge, and the second mountain fold reflects this reflection across its left edge. Thus, the top-left corner of Region 33 when the hole is punched will be the bottom-right corner when the paper is unfolded.
第一座山形折叠在其底部边缘反射区域 33 ，第二座山形折叠在其左侧边缘反射这个反射。因此，当孔被戳穿时，区域 33 的左上角将在纸张展开后成为底部右角。

Finally, the first mountain fold fixes Region 44 in place, and the second mountain fold reflects it across its left edge. Thus, the top-left corner of Region 44 when the hole is punched will be the top-right corner when the paper is unfolded.
最终，第一个山形折叠固定了区域 44 的位置，第二个山形折叠则将其沿左侧边缘翻折。因此，当在纸张上打孔时，区域 44 的左上角将变成展开后纸张的右上角。

Putting all this together, the positions of the holes when the paper is unfolded must be as shown above.
将所有这些放在一起，当纸张展开时，孔的位置必须如上所示。

If instead we valley-fold a square piece of paper in half, then mountain-fold the folded paper in half, and then punch a hole all the way through the multiple layers of folded paper, as shown above, where will the holes be when we unfold the paper?
如果我们将一张正方形的纸对折成山谷状，然后将折叠的纸再对折成山峰状，接着在多层折叠的纸中戳穿一个洞，直到穿透所有层，然后将纸展开，洞会在哪里？

A

B

C

D

Explanation 解释

To help see what’s going on, let’s label the four regions the folding divides the paper into.
为了帮助理解情况，让我们标记折叠将纸张分为的四个区域。

Let’s start with Region 1.1. The valley fold reflects Region 11 across its top edge, and the mountain fold then reflects this reflection across its right edge. Thus, the top-left corner of Region 11 when the hole is punched will be the bottom-right corner when the paper is unfolded.
让我们从区域 1.1. 开始。山谷褶皱在其顶部边缘反射区域 11 ，然后山褶皱在其右侧边缘反射这个反射。因此，当在纸张上打孔时，区域 11 的左上角将成为展开纸张后的右下角。

Next, let’s look at Region 2.2. The valley fold leaves Region 22 fixed in place, and the mountain fold then reflects Region 22 across its right edge. Thus, the top-left corner of Region 22 when the hole is punched will be the top-right corner when the paper is unfolded.
接下来，我们来看区域 2.2. 。山谷褶皱使区域 22 固定不动，然后山褶皱将其反射到右侧边缘。因此，当在纸张上打孔时，区域 22 的左上角将成为展开后纸张的右上角。

Both the valley fold and the mountain fold leave Region 33 fixed in place, as shown above, so the top-left corner of Region 33 when the hole is punched will be the top-left corner when the paper is unfolded.
山谷折叠和山折叠都将区域 33 固定在原位，如上图所示，因此在打孔后，区域 33 的左上角将与展开纸张后的左上角相同。

Finally, the valley fold reflects Region 44 across its top edge, and the mountain fold then fixes this reflection in place. Thus, the top-left corner of Region 44 when the hole is punched will be the bottom-left corner when the paper is unfolded.
最终，山谷折叠在其顶部边缘反射了区域 44 ，然后山折叠将这个反射固定在原位。因此，当在纸张上打孔时，区域 44 的左上角将变成展开后左下角的位置。

Putting all this together, the positions of the holes when the paper is unfolded must be as shown above.
将所有这些放在一起，当纸张展开时，孔的位置必须如上所示。

Two of the three hole patterns below were produced using the same procedure as in the previous two questions, differing only in the choice of whether to use a valley fold or a mountain fold in each of the first two steps.
在下面的三个孔图案中，有两个是使用了与前两个问题中相同的过程制作的，唯一不同的是在前两步中选择使用山谷折叠或山峰折叠。

Here are some instructions:
以下是几点说明：

• First, mountain-fold or valley-fold a square piece of paper in half so it’s a rectangle that is the same width but only half the height.
  首先，将一张正方形的纸对折成一半，形成一个宽度相同但高度只有原来一半的长方形。

• Next, mountain-fold or valley-fold this rectangle in half so it’s a square that is half the width and half the height of the original square.
  接下来，将这个矩形对折成山形或谷形，使其成为边长为原正方形一半的正方形。

• Finally, punch a hole in the top-left corner of the folded paper.
  最后，在折叠的纸张的左上角打一个孔。

Which one of these patterns could not have been made by following the instructions above?
这些模式中，哪一个可能是按照上述说明无法制作出来的？

A

B

C

Explanation 解释

Hole pattern A can be achieved with the folds shown above.
孔图案 A 可以通过上面所示的折叠实现。

And, similarly for hole pattern C.
同样地，对于孔图案 C。

However, there’s no way to make hole pattern B according to the procedure described above. Why not? The answer has to do with creases.

A crease always lies between exactly two regions of the paper. When the paper is folded, these regions become layers of the folded paper. Because of the crease, these layers are aligned with each other as though they have been “reflected” across the crease relative to each other.
折痕总是位于纸张的两个确切区域之间。当纸张折叠时，这些区域成为折叠纸张的层。由于折痕，这些层像被“反射”过一样相对于彼此对齐，沿着折痕。

That is, a point in one region is aligned with the point in the adjacent regions that correspond to the initial point’s “reflection” across the creases separating the initial region from the adjacent regions:
也就是说，在一个区域中的一个点与初始点在其与相邻区域分隔褶皱对面的对应点对齐：相邻区域中与初始区域分隔褶皱对面的点

In particular, this means that, for any folding with the crease pattern shown above (which every folding corresponding to our procedure must produce), regardless of the mountain-valley assignments for the creases, points in one region must be aligned with their reflections in both of the two adjacent regions.
特别是在特定情况下，这意味着对于任何生成了上方所示折痕模式的折叠（对应于我们程序的每个折叠都必须产生这种模式），无论折痕的山峰-山谷分配如何，一个区域中的点都必须与两个相邻区域中的反射点对齐。

For this crease pattern in particular, that means that the two lines must be lines of reflectional symmetry for any hole pattern that is produced.
对于这个折痕模式而言，这意味着任何产生的孔图案中的两条线都必须是反射对称线。

However, these two lines are not lines of reflectional symmetry for hole pattern B, so hole pattern B must not have been produced using our procedure.
然而，这两行并非孔型 B 的反射对称线，因此孔型 B 肯定不是通过我们的程序产生的。

If we mountain-fold a piece of paper in half 33 times and then punch a hole all the way through the multiple layers of the folded paper, as shown above, where will the holes be when we unfold the paper?
如果我们将一张纸山折 33 次，然后穿透多层折叠的纸张打孔，如下图所示，当我们展开纸张时，孔在哪里？

A

B

C

D

Explanation 解释

Before the hole is punched, the mountain-valley pattern for the folded paper matches the picture above.
在打孔之前，折叠纸张的山谷图案与上方的图片相匹配。

As discussed in the solution to the previous problem, when the paper is folded, creases are formed between the various regions. If two regions meet in a crease, then each point in one region must be aligned with the point in the other region corresponding to the reflection of the original point across the crease line.
如在解决上一个问题的方法中所述，当纸张折叠时，在各个区域之间会形成折痕。如果两个区域在折痕处相遇，那么一个区域内每个点都必须与折痕线对面区域中对应于原始点反射的点对齐。

This suggests a strategy for determining the hole pattern created by punching a hole in the folded paper.
这提出了一个策略，用于确定在折叠的纸上打孔所创建的孔图案。

First, pick a region where we know where the hole ends up. The top layer is a good choice, as shown above, since it’s fixed in place by all of the folds, so it’s in the same position when the paper is folded as it is when the paper is unfolded.
首先，选择一个我们知道洞最终所在的位置的区域。顶层是一个很好的选择，如下所示，因为它被所有的折痕固定在原位，所以在纸张折叠时和展开时都处于相同的位置。

Next, determine the position of the hole in one of the regions that meet this first region in a crease by reflecting the hole across this crease.
接下来，确定在与第一个区域在折痕处相交的区域之一中，孔的位置，通过将孔反射到该折痕上。

Repeat this process — that is, pick a pair of regions that meet in a crease where we know the position of the hole in one of the regions but not the other, and reflect the hole whose position we know across the crease — until we’ve found the positions of all the holes:
重复这个过程——也就是说，选择一对相交于褶皱处的区域，我们在这条褶皱上知道其中一个区域的洞的位置，但不知道另一个区域的洞的位置，然后将我们知道位置的洞反射到褶皱上——直到我们找到所有洞的位置：

If we mountain-fold a piece of paper in half 33 times and then valley-fold it, as shown above, where will the creases created by the valley fold be when we unfold the paper?
如果我们将一张纸山折 0#次，然后谷折，如下图所示，当我们展开纸张时，谷折产生的折痕会在哪里？

A

B

C

Explanation 解释

As discussed in the solutions to the previous problems, when the paper is folded, creases are formed between the various regions. If two regions meet in a crease, then each point in one region must be aligned with the point in the other region corresponding to the reflection of the original point across the crease line.
如在解决先前问题的方案中所述，当纸张折叠时，在各个区域之间会形成折痕。如果两个区域在折痕处相遇，那么一个区域内每个点都必须与另一个区域中对应于原始点沿折痕线反射的点对齐。

Since a crease line can be thought of as a collection of points, this suggests a strategy for determining where the valley fold creases end up.
由于折痕线可以视为一系列点的集合，这为确定山谷折叠折痕的最终位置提供了一种策略。

After the three mountain folds prior to the valley fold, the mountain-valley pattern matches the picture above.
在三个山脉褶皱之前，山谷褶皱，山脉-山谷模式与上方的图片相匹配。

Pick a region where we know what the valley fold does. The top layer after the mountain folds is a good choice, since it’s fixed in place by all of the mountain folds, so it’s in the same position when the paper is folded as it is when the paper is unfolded.
选择一个我们知道山谷褶皱作用的区域。山褶皱之后的顶层是一个不错的选择，因为它被所有山褶皱固定在原位，所以在纸张折叠时与展开时处于相同位置。

Next, pick a region that meets this first region in a crease, and determine the position of the crease line in the second region. To do this, reflect the crease in the first region across the crease separating the first region from the second region, as shown above.
接下来，选择一个区域，使其在折痕处与第一个区域相交，并确定第二区域中折痕线的位置。为此，将第一个区域的折痕沿分隔第一个区域和第二个区域的折痕进行镜像，如上图所示。

Repeat this — that is, pick a pair of regions that meet in a crease where we know the position of the valley fold crease in one of the regions but not the other, and reflect the valley fold crease whose position we know across the crease between the two regions — until we’ve found the positions of all the valley fold creases:
重复这个过程——也就是说，选择两个相交于折痕的区域，其中一个区域我们知道山谷折叠折痕的位置，而另一个区域不知道，然后将我们知道位置的山谷折叠折痕反射到两个区域之间的折痕上——直到我们找到所有山谷折叠折痕的位置：

If, after mountain-folding the paper in half 33 times, we make a cut instead of a fold along the line shown above, then we end up cutting a shape out of the middle of the paper.
如果，将纸张对折山折 33 次后，我们沿着上方所示的线进行切割而不是折叠，那么最终会在纸张中切割出一个形状。

If we mountain-fold a square piece of paper in half 33 times, as shown in the animation above, and then make a single straight-line cut perpendicular to the longest edge to the top edge of the folded paper, which of the two shapes could we possibly cut out?
如果我们将一张正方形纸张对折 mountain-fold 0# 次，如下图所示，然后沿着与最长边垂直的直线在折叠纸张的顶部边缘处剪切，我们可能剪出的两个形状中的哪一个？

Note: The cut must go through all the layers of the folded paper.
注意：剪切必须穿过折叠纸的所有层。

A only A 只有

B only B 只有

Both A and B A 和 B

Neither A nor B 既非 A 也非 B

Explanation 解释

It’s possible to cut out shape A, as shown above. However, it’s not possible to cut out shape B:
可以裁剪出形状 A，如上所示。然而，无法裁剪出形状 B：

The edges of whatever shape we cut out must correspond to the cut lines in each of the regions of the paper. But the cut line in one region must be the reflection across the crease lines of the cut lines in the adjacent regions.
我们剪出的任何形状的边缘都必须对应于纸张上每个区域的剪切线。但是，一个区域中的剪切线必须是相邻区域中剪切线沿折痕线的反射。

Since the regions are all congruent, the cut lines in each region should be congruent as well. This implies that all the edges of the shape we cut out must be the same length — however, shape B has edges of different lengths, so it’s not possible to cut it out.
由于所有区域都是相等的，因此每个区域中的切割线也应该是相等的。这意味着我们剪出的形状的所有边都应该是相同长度——然而，形状 B 的边有不同长度，所以无法剪出它。

2D Single-Vertex Flat Folding (I)

二维单顶点平面折叠（I）

If we fold a circular piece of paper, as shown in the first image above, and then unfold it, what will the mountain-valley pattern look like?
如果我们将一张圆形的纸张折叠，如下图所示，然后展开它，山谷图案会是什么样的？

A

B

C

D

Explanation 解释

After the first mountain fold, there are two layers of paper, one on top of the other. The two layers exactly coincide, but they’re facing different directions. This is similar to the situation we encountered when we valley-folded the 1D1D strip of paper in half.
在第一次山形折叠之后，有两层纸，一层在另一层之上。两层完全重合，但方向不同。这类似于我们用 1D1D 纸条对折时遇到的情况。

The effect of this is that the creases on the top layer appear on the bottom layer as though they were reflected across the crease line. Also, just as when we valley-folded the 1D1D strip of paper in half, since the layers are facing different directions, a mountain crease on the top layer appears as a valley crease on the bottom layer.
这种效果是，顶层的折痕在底层看起来像是沿着折痕线反射的。同样，就像我们对折 1D1D 纸条时一样，由于层的方向不同，顶层的山形折痕在底层表现为山谷折痕。

Putting this together, the mountain-valley pattern on the upper half of the circle — which was the bottom layer after the first mountain fold — should be a reflection of the mountain-valley pattern on the lower half of the circle, but with a valley crease instead of a mountain crease. Thus, the correct answer must be D:
将这些放在一起，圆的上半部分的山谷模式——这是第一次折叠后的底层——应该反映圆的下半部分的山谷模式，但用山谷折痕代替山折痕。因此，正确的答案必须是 D:

One way to produce the mountain-valley pattern from the previous problem is to start with the crease pattern shown on the left and then to make mountain-valley assignments for each of the 44 creases between the edge of the paper and the center. So, creases 1,3,1,3, and 44 become mountain creases and crease 22 becomes a valley crease.
一种产生上一个问题中提到的山谷模式的方法是从左边显示的折痕模式开始，然后为纸张边缘和中心之间的每个 44 折痕进行山峰-山谷分配。因此，折痕 1,3,1,3, 和 44 变为山峰折痕，折痕 22 变为山谷折痕。

Just as in the 1D1D case, given a crease pattern, if it’s possible to produce a flat-foldable mountain-valley pattern by making mountain-valley assignments for each of the creases in the crease pattern, then we’ll call the original crease pattern flat-foldable. As in the 1D1D case, however, this doesn’t mean that every mountain-valley pattern for that crease pattern is flat-foldable — only that there’s at least one mountain-valley pattern that is flat-foldable.
正如在 1D1D 的情况下，给定一个折痕模式，如果可以通过为折痕模式中的每个折痕进行山峰-山谷分配来产生一个可平面折叠的山峰-山谷模式，那么我们就会称原始折痕模式为可平面折叠的。然而，正如在 1D1D 的情况下，这并不意味着该折痕模式下的每个山峰-山谷模式都是可平面折叠的——只是至少存在一个可平面折叠的山峰-山谷模式。

When folding in 1D,1D, we found that every crease pattern was flat-foldable. In 2D,2D, the situation is a bit more complicated. Even if all the creases meet in a single vertex (as will be the case in this lesson), a crease pattern may not be flat-foldable.
当我们加入 1D,1D, 时，我们发现每一种折痕模式都是可平面折叠的。在 2D,2D, 中，情况稍微复杂一些。即使所有折痕都集中在单个顶点（正如本课中将发生的那样），折痕模式可能仍然不可平面折叠。

Each of the crease patterns in the top row is flat-foldable, but none of the crease patterns in the bottom row are flat-foldable.
上排中的每一种折痕模式都可以平面折叠，但下排中的任何一种折痕模式都无法平面折叠。

In this lesson and the next one, we’ll explore necessary and sufficient conditions for a single-vertex crease pattern to be flat-foldable. By the time we’re finished, we’ll be able to tell whether a crease pattern is flat-foldable just by looking at it.
在这节课和下节课中，我们将探讨单顶点折痕模式平折叠的必要和充分条件。到我们完成时，仅通过观察，我们就能判断折痕模式是否可以平折叠。

To flat-fold the mountain-valley pattern on the right, pre-crease each crease and then tuck regions 22 and 33 between regions 11 and 4:4:
将右侧的山谷图案压平折叠，预先折痕每一处折痕，然后在区域 11 和区域 4:4: 之间的区域 22 和 33 处藏起部分

As this example demonstrates, a mountain-valley pattern can be flat-foldable even if it’s not possible to fold it by making a series of folds from one edge of the paper to the other.
正如这个例子所示，即使无法通过从纸的一边折叠到另一边来折叠，山谷模式也可以平面折叠。

Looked at from overhead, the two flat-foldings of the mountain-valley patterns shown above look similar — each is a 120∘120∘ wedge. However, if you look at them from the side so you can see their layers, it’s possible to tell them apart:
从上方看，上述山脉模式的两个平面折叠看起来相似——每一个是 120∘120∘ 楔形。但是，如果你从侧面看，可以看到它们的层，从而区分它们：

A.

B.

In which of the options above is each mountain-valley pattern matched with the appropriate side view?
在上述选项中，每一种山谷模式与适当的侧视图相匹配的是哪一个？

A

B

Explanation 解释

The top folding should have the two shorter layers folded under the two longer layers, while the bottom folding should have the two shorter layers folded between the two longer layers.
顶部折叠应使两个较短的层折叠在两个较长的层之下，而底部折叠应使两个较短的层折叠在两个较长的层之间。

Every flat-foldable mountain-valley pattern for a circular piece of paper where all the creases go from the edge to the center of the circle will produce a multi-layered wedge when the paper is folded flat. Moreover, every point on the edge of the paper will lie somewhere along the arc of one of the layers of the wedge. This means that when we look at the folded paper from the side, we can see every point on the edge of the paper:
每一张圆形纸片，所有折痕从边缘到圆心，当纸张被平折时，都会产生多层楔形结构。此外，纸张边缘的每一个点都将位于楔形结构某一层的弧线上。这意味着，当我们从侧面观察折叠后的纸张时，可以看到纸张边缘上的每一个点。

Because of perspective, when we view the folded paper from the side, the lengths of the layers will not necessarily correspond to the lengths of their arcs. It’ll be convenient for us to ignore perspective and focus instead on arc lengths — so, in our “side view” images, the length of each layer will correspond to the length of its arc, which will in turn be proportional to the measure of its central angle.
由于视角的原因，当我们从侧面观察折叠的纸张时，层的长度并不一定与它们的弧长相对应。为了方便，我们可以忽略视角，转而关注弧长——因此，在我们的“侧面视图”图像中，每层的长度将对应于其弧的长度，而这反过来又与它的中心角的度量成比例。

Imagine an ant walking along the edge of a circular piece of paper flat-folded, as shown above, starting at the top layer.
设想一只蚂蚁沿着一张平折成圆形的纸片的边缘行走，如上图所示，从顶层开始。

From the side view, as the ant traverses the edge of the top layer (or, equivalently, the first arc), it appears to be walking right. In traversing the first arc, the ant walks 120∘120∘ counterclockwise.
从侧面看，当蚂蚁穿越顶层的边缘（或者说，第一个弧线）时，它看起来像是向右行走。在穿越第一个弧线时，蚂蚁以 120∘120∘ 逆时针方向行走。

After the ant passes the first crease (a mountain crease), it moves to the second layer — or, equivalently, the second arc. It changes direction, and from the side view, it now appears to be walking left. In traversing the second arc, the ant walks 60∘60∘ clockwise. Note that while the arrow showing the ant’s path around the circle is still counterclockwise, the ant is going clockwise because this layer has been folded over so its orientation is reversed.
蚂蚁经过第一个褶皱（一座山的褶皱）后，移动到第二层——或者说，第二条弧线。它改变了方向，从侧面看，现在似乎是在向左行走。在穿越第二条弧线时，蚂蚁以 60∘60∘ 顺时针方向行走。请注意，虽然指示蚂蚁路径的箭头仍然逆时针方向，但蚂蚁实际上是在顺时针方向行走，因为这一层已经被折叠，其方向因此被反转。

Next, the ant passes the second crease — a valley crease — and moves to the third layer/arc. It again changes direction, and from the side view, it appears to be walking right. In traversing the third arc, the ant walks 60∘60∘ counterclockwise.
接下来，蚂蚁通过第二个折痕——一个山谷折痕——并移动到第三层/弧。它再次改变方向，从侧面看，它似乎在向右行走。在穿越第三个弧时，蚂蚁以 60∘60∘ 逆时针方向行走。

The ant passes the third crease — a mountain crease — and moves to the bottom layer, the fourth and final arc. It changes direction, so it appears to be walking left. In traversing the fourth arc, the ant walks 120∘120∘ clockwise.
蚂蚁穿越第三个褶皱——一个山褶皱——并移动到下一层，第四和最终的弧线。它改变了方向，所以看起来是在向左行走。在穿越第四弧线时，蚂蚁以 120∘120∘ 顺时针方向行走。

A.

B.

Which one could be a side view of a flat-folding of the mountain-valley pattern shown above?
哪一个是上方所示山川图案的平面折叠侧视图？

Only A 只有 A

Only B 只有 B

Both A and B A 和 B

Neither A nor B 既非 A 也非 B

Imagine an ant walking along the edge of a circular piece of paper that has been flat-folded so that all the creases go from the edge of the paper to the center.
设想一只蚂蚁沿着一张被平折叠成圆形的纸张边缘行走，所有折痕都从纸张的边缘指向中心。

If the ant is currently moving clockwise, what direction will it be going after it passes the next crease?
如果蚂蚁当前正在顺时针移动，那么在它经过下一个折痕后会朝什么方向移动？

Clockwise 顺时针

Counterclockwise 逆时针

It depends whether the next crease is a mountain crease or a valley crease.
这取决于下一个折痕是山形折痕还是山谷折痕。

When we go for a hike, no matter what path we take, when we return to our starting point,
当我们去远足时，无论我们走哪条路，当我们回到起点时，

• we must have traveled the same distance north as we’ve traveled south,
  我们必须向北行驶的距离与向南行驶的距离相同

• we must have traveled the same distance west as we’ve traveled east, and  

• we must have traveled the same distance up as we’ve traveled down.
  我们必须上行的距离和下行的距离相等。

Similarly, an ant that walks all the way around the edge of a single-vertex, flat-folded piece of circular paper must ultimately travel the same distance clockwise as it travels counterclockwise.  

As we saw earlier, an ant walking along the edge of the flat-folding on the left, starting at the left edge of the top layer, walks 120∘120∘ counterclockwise, then 60∘60∘ clockwise, then 60∘60∘ counterclockwise, and finally 120∘120∘ clockwise, so the net counterclockwise distance the ant travels is  

120∘−60∘+60∘−120∘=0∘.120∘−60∘+60∘−120∘=0∘.

That is, the ant walks the exact same distance clockwise as counterclockwise, exactly as it should.  

Likewise, for an ant walking along the edge of this piece of paper, again starting at the left edge of the top layer and walking right, the net counterclockwise distance is  

90∘−60∘+45∘−60∘+45∘−60∘=0∘.90∘−60∘+45∘−60∘+45∘−60∘=0∘.

What happens when this alternating sum is not equal to 0∘?0∘?  

Is the crease pattern above flat-foldable?  

Yes  No  

Explanation 解释

The alternating sum of the angle measures of the arcs of this crease pattern is  

120∘−60∘+90∘−90∘=60∘,120∘−60∘+90∘−90∘=60∘,

or alternatively,  

60∘−90∘+90∘−120∘=−60∘.60∘−90∘+90∘−120∘=−60∘.

In particular, it’s not equal to 0∘.0∘. That means that if there were a flat-folding of this crease pattern, then an ant walking all the way around the edge of the paper would end up walking further counterclockwise than clockwise, or vice-versa. But this is not possible since when the ant has walked all the way around the edge of the paper, it must be back where it started — so, it must have walked the same distance counterclockwise as clockwise.  

Thus, our assumption that there was a flat-folding must have been incorrect, so there’s no possible flat-folding of this crease pattern. This is a significant contrast with the 1D1D case where every crease pattern was flat-foldable.  

The alternating sum of the angle measures of the arcs of this crease pattern is  

120∘−60∘+90∘−90∘=60∘,120∘−60∘+90∘−90∘=60∘,

or alternatively,  

60∘−90∘+90∘−120∘=−60∘.60∘−90∘+90∘−120∘=−60∘.

In particular, it’s not equal to 0∘.0∘. That means that if there were a flat-folding of this crease pattern, then an ant walking all the way around the edge of the paper would end up walking further counterclockwise than clockwise, or vice-versa. But this is not possible since when the ant has walked all the way around the edge of the paper, it must be back where it started — so, it must have walked the same distance counterclockwise as clockwise.  

Thus, our assumption that there was a flat-folding must have been incorrect, so there’s no possible flat-folding of this crease pattern. This is a significant contrast with the 1D1D where every crease pattern was flat-foldable.  

The same holds true for every crease pattern:   

If the alternating sum of the angle measures isn’t equal to 0∘,0∘, the crease pattern isn’t flat-foldable.  

As we’ve seen, if the alternating sum of the angle measures of a crease pattern isn’t equal to 0∘,0∘, then the crease pattern isn’t flat-foldable. Additionally, if a crease pattern has an odd number of creases, then it’s not flat-foldable.  

One way to see this is to again consider an ant walking along the edge of a flat-folded piece of paper. As we’ve seen, each time the ant passes a crease, it changes direction — from clockwise to counterclockwise or vice-versa — regardless of whether the crease is a mountain crease or a valley crease.  

So, imagine the ant starts out from some point along the edge of the paper. To be concrete, let’s assume the ant is going counterclockwise. After it passes the first crease, it switches to clockwise. After the second crease, it switches back to counterclockwise, and so on. In particular, if it has passed an even number of creases, it’ll be going counterclockwise, and if it has passed an odd number of creases, it’ll be going clockwise.  

When the ant gets all the way back to where it started, it must have passed each crease exactly once. But also, since it started out going counterclockwise, it must be going counterclockwise. That means that it must have passed an even number of creases, so the total number of creases must be an even number.

2D Single-Vertex Flat Folding (II)

So, now we know that if a single-vertex crease pattern doesn’t have an even number of creases or the alternating sum of the angles between consecutive creases isn’t equal to 0,0, then the crease pattern is not flat-foldable.

But what if a single-vertex crease pattern does meet those conditions? Can we be certain that it is flat-foldable?

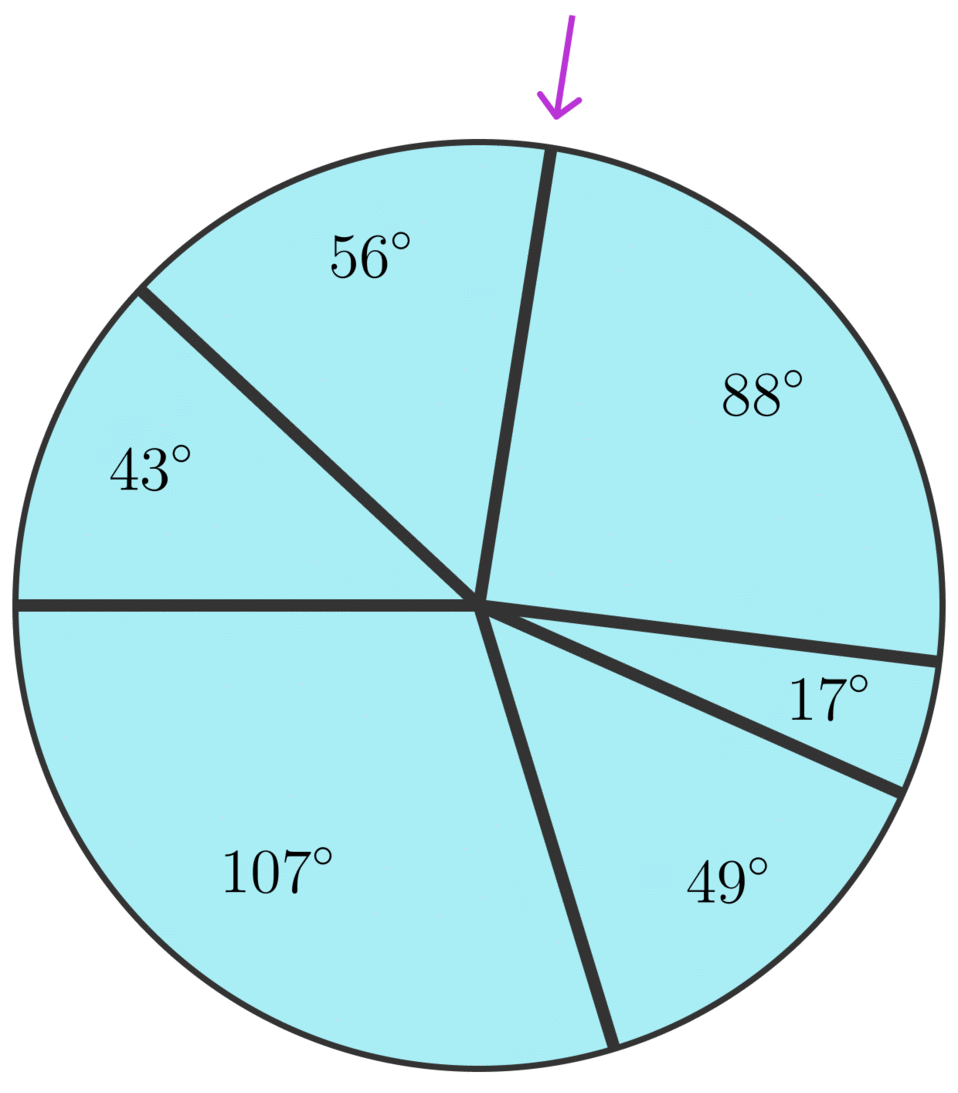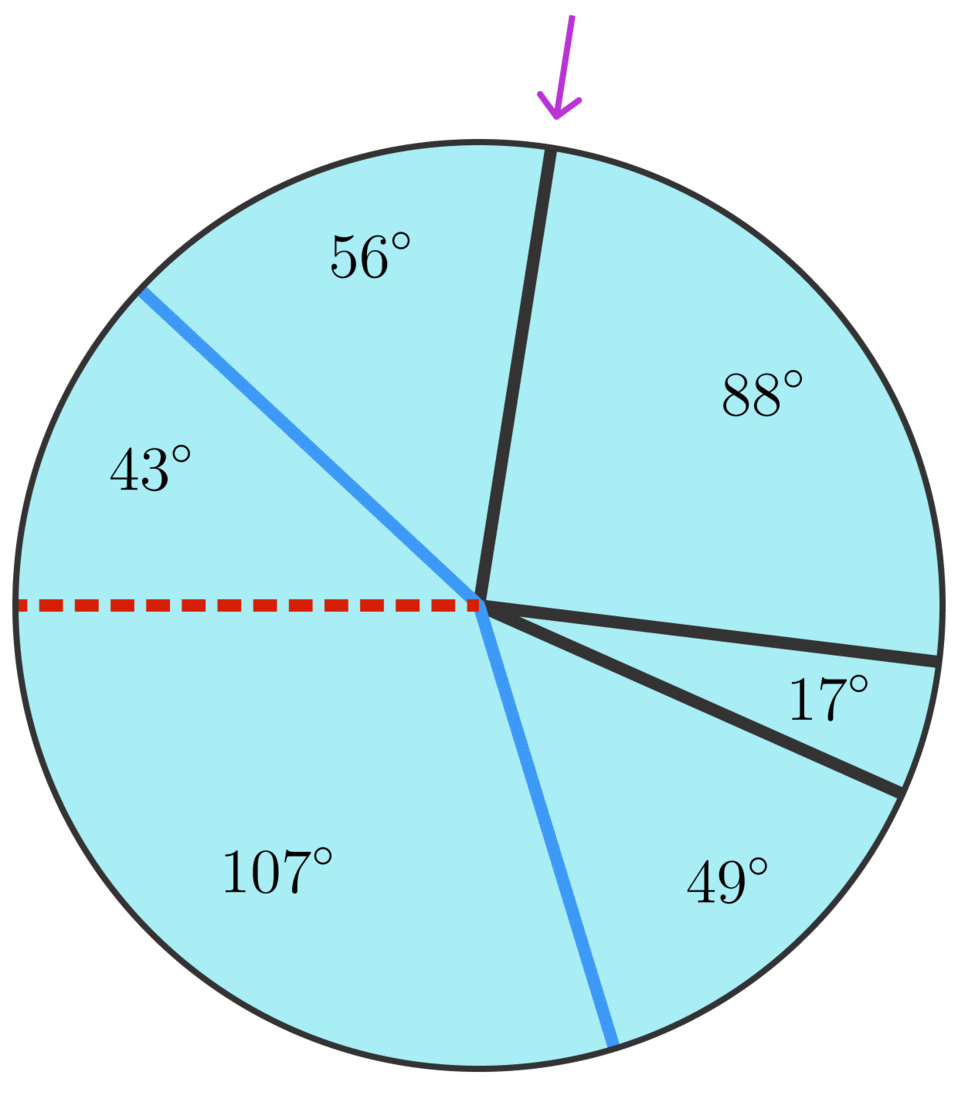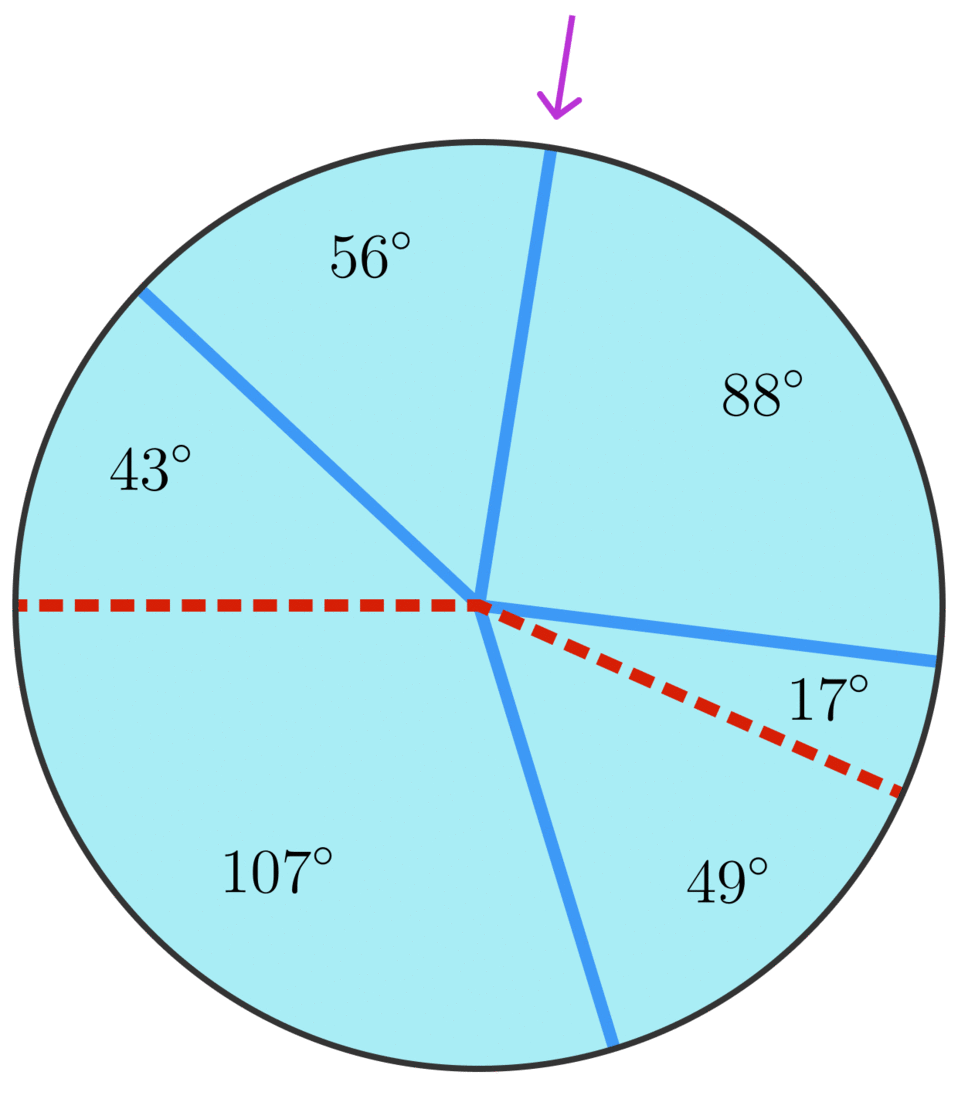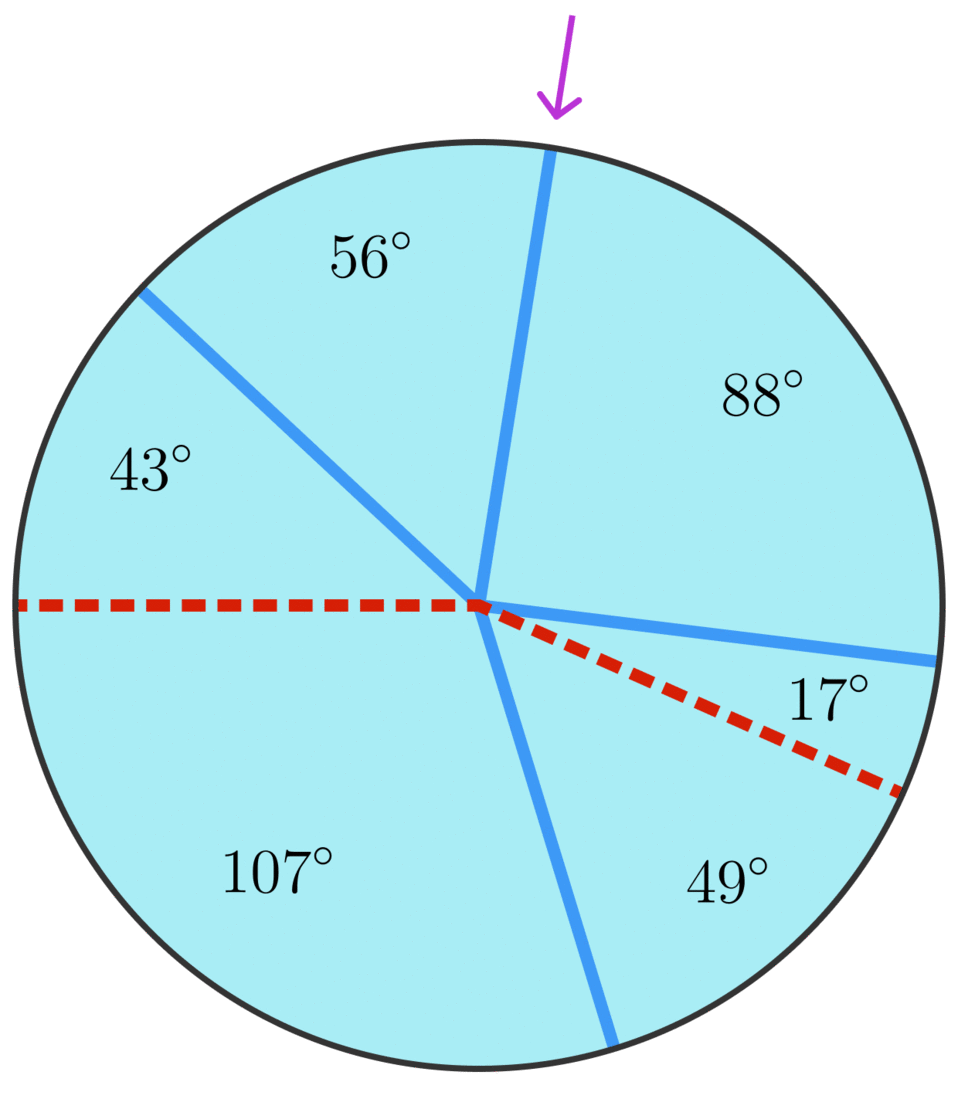
Imagine that a circular piece of paper has been divided into a series of arcs, as shown above, and imagine that an ant starts at the position indicated in the image above and walks counterclockwise around the edge of the circle — note that the paper is not folded. As the ant makes its way around the circle, it carries out this procedure:

• Before departing, the ant writes down the number 0.0.

• After completing the first arc, the ant adds the angle measure in degrees of the arc to 0:0: that is, 0+107=107.0+107=107.

• When the ant reaches the second arc, it subtracts the angle measure of this arc from its running total, obtaining 107−49=58.107−49=58.

• When the ant reaches the third arc, it adds the angle measure of this arc to its running total, obtaining 58+17=75.58+17=75.

The ant continues in this way, adding the angle measures of the odd arcs and subtracting the angle measures of the even arcs, until it reaches the sixth and final arc. As it does so, it forms this sequence of alternating partial sums:

0+107=107107−49=5858+17=7575−88=−13−13+56=4343−43=0.0+107107−4958+1775−88−13+5643−43​=107=58=75=−13=43=0.​

Is it possible for the ant to pick a starting arc so that every partial sum in the sequence is non-negative?

Yes

No

Why?

Explanation

The alternating partial sums first become negative after 88∘,88∘, so let’s start with the first arc after the 88∘88∘ arc, the 56∘56∘ arc:

0+56=5656−43=1313+107=120120−49=7171+17=8888−88=0.0+5656−4313+107120−4971+1788−88​=56=13=120=71=88=0.​

These alternating partial sums are all non-negative.

Note: The 49∘49∘ arc also works.

Suppose we use the division of the circle into arcs in the previous problem to define a crease pattern. Then the alternating partial sums starting at the crease indicated in the picture are always non-negative. We’ll use this fact to make a mountain-valley assignment for the crease pattern:

• Start at the crease indicated in the picture above. Call this the starting crease.

• Make the first crease after the starting crease in the counterclockwise direction a mountain crease.

• Make the next crease a valley crease.

• Continue to alternate mountain and valley creases in the counterclockwise direction until there’s only one unassigned crease left — which will be the starting crease. Even though this crease will be bounded by mountain creases, make it a mountain crease.

When we finish, we’ll have the mountain-valley pattern shown above. This mountain-valley pattern produces a flat-folding of the paper:

In the flat-folding pictured above, the 56∘56∘ arc is the top layer, followed by the 43∘43∘ arc, and so on.

Which of the crease patterns above is flat-foldable?

A only

B only

Both A and B

Neither A nor B

Why?

Explanation

We can immediately discard B since the alternating sum of its angles isn’t equal to 0:0:

90−30+90−60+30−60=60.90−30+90−60+30−60=60.

By contrast, the alternating sum of the angles of A is equal to 0:0:

90−60+30−90+60−30=0.90−60+30−90+60−30=0.

Further, if we start at one of the 60∘60∘ arcs and go counterclockwise, the alternating partial sums are all non-negative:

0+60=6060−30=3030+90=120120−60=6060+30=9090−90=0.0+6060−3030+90120−6060+3090−90​=60=30=120=60=90=0.​

This suggests we can use the same procedure we implemented previously to produce a flat-foldable mountain-valley pattern:

• Pick one of the 60∘60∘ arcs, and make the starting crease the crease that is the clockwise border of this arc.

• Make the first crease after the starting crease in the counterclockwise direction a mountain crease.

• Make the next crease a valley crease.

• Continue to alternate mountain and valley creases in the counterclockwise direction until there’s only one unassigned crease left — which will be the starting crease. Make this last crease a mountain crease.

Let’s go back and take a closer look at the procedure we implemented to find a flat folding of a crease pattern. Why does it work?

The key idea is that folding a circular piece of paper so that all the creases go from the edge to the center is actually quite similar to folding a 1D1D strip of paper. The folding of the 2D2D circle is totally determined by how the edge of the circle folds up, and the edge of the circle is like a 1D1D line segment whose ends have been tied together.

When folding 1D1D strips, alternating between mountain and valley creases creates a zigzag shape where the layers never collide, as in the picture above. If the first crease is a mountain crease, each layer is below the preceding layer — if the first crease is a valley crease, each layer is above the preceding layer. Thus, every 1D1D crease pattern can be flat-folded via a mountain-valley assignment with alternating mountain and valley creases.

Something similar works for circles, but with a little additional complexity.

Suppose we want to flat-fold the crease pattern shown above.

One thing we could try, recalling our strategy for flat-folding a 1D1D strip, is to pick an arc — let’s say the 88∘88∘ arc — to be the top layer and then alternate mountain and valley creases so the arcs form a zigzag shape underneath the top layer. This ensures that none of the subsequent layers will collide. But there’s one thing we have to watch out for — since the edge of a circle is like a line segment whose ends have been tied together, the bottom layer must be connected to the top layer. In the picture above, this is not possible because there are layers that get in the way.

In particular, the problem is that there are layers that extend farther to the left — that is, farther in the clockwise direction — than the left end of the top layer. This corresponds to the alternating partial sums going negative:

  0+88=8888−56=3232+43=7575−107=−32−32+49=1717−17=0.  0+8888−5632+4375−107−32+4917−17​=88=32=75=−32=17=0.​

In particular, the alternating partial sums give the ant’s net counterclockwise distance traveled after walking each arc. If there’s a positive partial sum followed by a negative partial sum as in the case of 7575 and −32−32 above, then there’s an arc that, when folded, becomes a layer with one edge on each side of the starting point, so this layer will get in the way of the bottom layer connecting with the top layer.

The trick then is to pick a starting arc so that the alternating partial sums are always non-negative. This ensures that we’ll be able to connect the bottom layer to the top layer without any intermediate layers getting in the way. This is precisely what we did in the procedure:

• we found an arc such that the alternating partial sums starting at that arc were always non-negative,

• we alternated mountain and valley creases starting at one end of that arc, causing the subsequent layers to form a zigzag shape that stayed to the right of the left edge of the top layer, and then

• we made a final crease that connected the bottom layer to the top layer, and we were done.

Given a single-vertex crease pattern with an even number of creases where the alternating sum of the angle measures is equal to 0,0, it’s always possible to find a crease such that the alternating partial sums of the angle measures starting at that crease are all non-negative. This means that every single-vertex crease pattern with an even number of creases where the alternating sum of the angle measures is equal to 00 is flat-foldable.

Thus, given a single-vertex crease pattern, we can determine whether or not the crease pattern is flat-foldable using only information about the number of creases and the measures of the angles:

• If the number of creases is even and the alternating sum of the angle measures is equal to 0,0, the crease pattern is flat-foldable.

• If not, the crease pattern isn’t flat-foldable.

Is this crease pattern flat-foldable?

Yes

No

Why?

Explanation

Let’s check the alternating sum of the angles:

67−27+33−58+75−37+22−41=34,67−27+33−58+75−37+22−41=34,

so this crease pattern isn’t flat-foldable.

This crease pattern isn’t flat-foldable. Is it possible to make a flat-foldable crease pattern by adding exactly one more crease?

Note: Like the other creases, the crease we add must go from the edge to the center.

Yes

No

Why?

Explanation

This crease pattern has 88 creases, so adding another crease would give it an odd number of creases. Since no single-vertex crease pattern with an odd number of creases is flat-foldable, it’s not possible to make a flat-foldable crease pattern by adding one more crease.

Is it possible to make a flat-foldable crease pattern by rotating one crease about the center of the circle?

Note: The crease we rotate must stay between the two neighboring creases.

Yes

No

Why?

Explanation

When we computed the alternating sum, the sum of the angles of the 67∘,67∘, 33∘,33∘, 75∘,75∘, and 22∘22∘ arcs was 34∘34∘ greater than the sum of the 27∘,27∘, 58∘,58∘, 37∘,37∘, and 41∘41∘ arcs. This suggests that if we rotate one of the creases 17∘17∘ about the center to reduce one of the arcs in the first group and augment one of the arcs in the second group, the alternating sum will be equal to 0.0.

We could achieve this with any of the arcs. Below is one example:

Since the alternating sum is equal to 0,0, this crease pattern must be flat-foldable — and we even have a procedure to do it.

Strange Polygons 奇怪的多边形

Polygons are two-dimensional — or “flat” — shapes that are bounded by straight edges around an interior region with no holes.
多边形是二维的——或者说“平面的”——形状，由直线边围绕一个内部区域组成，且没有孔洞。

Which of the figures above is an irregular polygon?
以上哪一个是不规则多边形？

Figure A 图 A

Figure B 图 B

Figure C 图 C

None of them are polygons.
他们都不是多边形。

Frequently, geometry classes will avoid covering irregular polygons, or they’ll only cover specific cases like rectangles and right triangles but have little to say about crazy-looking shapes like this irregular triacontakaioctagon — a 3838-sided polygon:
经常，几何课程会避免讨论不规则多边形，或者仅会覆盖特定情况，如矩形和直角三角形，而对于这种看起来很奇特的不规则三十二边形——一个 3838 边的多边形——则很少涉及

But there are many interesting applications of designing crazy-looking irregular polygons!
但有许多有趣的用途是设计看起来疯狂的不规则多边形！

The lessons in this chapter will cover two of these applications in depth:
本章的课程将深入探讨这两个应用：

• the art gallery problem and
  艺术画廊问题和

• Pick’s theorem — pegboard polygons.
  泊松定理——针板多边形。

An Example Art Gallery Puzzle:
一个示例艺术画廊谜题：

The irregular purple polygon above is the floor plan of a gallery, and an example is shown of what could be seen by a single guard in a given location.
上方的不规则紫色多边形是画廊的平面图，展示了一个特定位置的单个守卫可能看到的示例。

Our job is to position some number of unmoving guards — who cannot see through walls — so that every location in the gallery is in view of one of the guards.
我们的任务是布置一定数量的不动守卫——他们无法穿透墙壁——使得画廊中的每一个位置都能被一个守卫看到。

What’s the fewest number of guards that you could use?
你能用的最少的守卫数量是多少？

11

22

33

44

Explanation 解释

The two images above illustrate how to guard the whole gallery using two guards and why using at least two guards is necessary.

Why are at least two guards necessary?

If we consider the corner with the red dot (imagine that there’s a piece of cake there that must be very carefully guarded), then the red region is every position in the gallery that has a line of sight to that spot. Therefore, a guard must be positioned somewhere inside or on the border of the red region, or the cake won’t be visible to any guard.
如果我们考虑那个有红点的角落（想象一下，那里有一块必须非常小心守护的蛋糕），那么红色区域就是画廊中每一个能看到那个位置的位置。因此，必须在红色区域的内部或边界处布置一个守卫，否则任何守卫都无法看到蛋糕。

Similarly, the green region is every position in the gallery that has a line of sight to the corner where a delicious doughnut is displayed, so a guard must be positioned within or on the border of the green region, or the doughnut won’t be visible to any guard.
同样地，绿色区域指的是画廊中每一个可以看到摆放美味甜甜圈角落的位置，因此必须在绿色区域内部或边界处布置一名警卫，否则任何警卫都无法看到甜甜圈。

Because the red and green regions don’t overlap, we can conclude that at least two guards will be needed to guard this gallery — one within or on the border of the red region, and another within or on the border of the green region.
由于红色和绿色区域没有重叠，我们可以得出结论，至少需要两名警卫来守护这个画廊——一名位于或在红色区域的边界内，另一名位于或在绿色区域的边界内。

Why are two guards sufficient?

The right image above illustrates one way to place two guards so that at least one of them has a line of sight to every position in the gallery.
上图右侧展示了放置两名守卫的一种方式，确保至少一名守卫能够看到画廊中的每一个位置。

In the figure above, the black dots are one unit apart vertically and horizontally. What’s the area of the portion shaded blue?
在上图中，垂直和水平方向上黑色点之间的距离为一个单位。蓝色部分的面积是多少？

22

44

88

1616

Some definitions of “polygon” aim to exclude shapes like the ones below and some aim to include them — but we want to exclude them:
一些“多边形”的定义旨在排除下图所示的形状，而有些定义则试图包含它们——但我们想排除这些形状：

So, we won’t consider figures like these in the remainder of the lessons — we’re going to restrict to a smaller collection of polygons called simple polygons. This definition will, of course, exclude all of the strange shapes above.
因此，在接下来的课程中，我们不会考虑这些数字——我们将限制在称为简单多边形的小型集合中。当然，这个定义将排除上面的所有奇怪形状。

A polygon is simple if it meets these two additional constraints:
一个多边形如果满足这两个额外的约束条件：

• The edges only intersect at their endpoints — each of these intersections is called a vertex.
  边仅在端点处相交——每个这些交点称为顶点。

• Every vertex is an intersection of exactly two edges.
  每个顶点恰好是两条边的交点。

Here’s a simple polygon: 这是一个简单的多边形：

Which part of our definition makes it clear that the figure above is not a simple polygon?
哪一部分的定义明确指出上图不是简单多边形？

It’s two-dimensional. 它是二维的。

Its boundary is a circuit of straight edges.
它的边界是一个由直线组成的环。

The circuit of edges bounds a closed interior region.
电路中的边形成一个封闭的内部区域。

The edges only intersect at their endpoints.
边线仅在端点处相交。

Every vertex is an intersection of exactly two edges.
每个顶点恰好是两条边的交点。

Explanation 解释

We can check each part of the definition separately:
我们可以分别检查定义的每个部分：

1. The shape is clearly two-dimensional.
   形状显然是二维的。

2. The shape’s boundary is a circuit of straight edges since we can number the edges to create a circuit:
   形状的边界是一个由直线组成的回路，因为我们可以通过编号边来创建一个回路：

   

3. The circuit of edges bounds a closed interior region, which is indicated by the purple interior:
   电路中的边形成一个封闭的内部区域，该区域由紫色内部表示：

   

4. The edges only intersect at their endpoints, which are marked in red:
   边缘仅在端点处相交，端点用红色标记：

   

5. Since there’s a vertex where four edges intersect, as shown in red below, the shape fails to meet the constraint that every vertex is an intersection of exactly two edges to be a simple polygon:
   由于存在四条边相交的顶点，如下图所示为红色标记的部分，该形状无法满足简单多边形的约束条件，即每个顶点恰好是两条边的交点

   

Lastly, in these lessons, we’ll also talk about a special kind of polygon called an orthogonal polygon. An orthogonal polygon is a polygon with the property that every internal angle measures either exactly 90∘90∘ or exactly 270∘.270∘.
最后，在这些课程中，我们还将讨论一种特殊的多边形，称为正交多边形。正交多边形是一种具有每个多边形内部角度恰好为 0 度或恰好为 180 度的性质的多边形。

How many of the internal angles of the orthogonal polygon above are reflex angles — angles with a measure between 180∘180∘ and 360∘?360∘?
上述直角多边形的内部角度中有多少是折角——度数在 180∘180∘ 和 360∘?360∘? 之间的角度？

66

1010

1616

2020

Orthogonal polygons are interesting special cases for both Pick’s theorem and for the art gallery problem. The next several lessons will explore art gallery challenges, and then the final four lessons in Irregular Polygons will switch over and explore Pick’s theorem:
正交多边形对于 Pick 定理和画廊问题都是有趣的专业案例。接下来的几节课将探讨画廊挑战，然后在不规则多边形的最后四节课中，我们将转向并探索 Pick 定理。

Convex vs. Concave 凸形 vs. 凹形

In these lessons, we’re focusing almost exclusively on irregularly-shaped art galleries. This isn’t just to be contrary, it’s because the regular-polygon cases are all fairly boring. Let’s look at this example:
在这些课程中，我们几乎完全专注于不规则形状的艺术画廊。这不是为了逆反，而是因为正多边形的情况都相当乏味。让我们来看这个例子：

True or False? 真假？

No matter where you put a guard in this regular pentagon, he will be able to see the entirety of the inside of the pentagon.
不管你在这个正五边形的任何位置放置一个守卫，他都能看到五边形内部的全部。

Recall that guards may not move, but they are allowed to turn to look at any angle.
回想一下，守卫不能移动，但他们被允许转向以查看任何角度。

True 真

False 假

Explanation 解释

It’s true that no matter where a guard is placed, he’ll be able to see the entirety of the inside of the pentagon.
确实，无论将守卫放置在哪里，他都能看到五角大楼内部的全部。

Any point inside of the pentagon has a direct line of sight to all of the sides and corners of the pentagon, so a guard placed anywhere inside the pentagon will be able to see the whole gallery:
任何五边形内部的点都可以直接视线到达五边形的所有边和角，因此，放置在五边形内部的任何位置的警卫都将能看到整个画廊：

There’s actually a special name for polygons that can be guarded by one guard positioned anywhere in the gallery. That name is convex.
其实有一种特殊的多边形名称，指的是可以由放置在画廊任何位置的单一守卫守护的多边形。这个名称是凸多边形。

A simple polygon is convex if every straight line segment connecting any two points on the perimeter never travels outside of the polygon.
简单多边形如果每条连接边界上任意两点的直线段从未离开多边形，则该多边形是凸的。

A simple polygon is concave if it’s not convex.
简单多边形如果不是凸形的，就是凹形的。

Which of the polygons above is convex?
上述哪个多边形是凸多边形？

A

B

C

D

Explanation 解释

For figures A, C, and D, it’s possible to find a line connecting two points on the perimeter that travels outside the polygon, so these shapes are concave, not convex.
对于图 A、C 和 D，有可能找到连接多边形外部的两点的线，因此这些形状是凹形的，而不是凸形的。

For figure B, any line connecting two points on the perimeter is contained completely in the polygon, so it’s convex.
对于图 B，连接边界上两点的任何线段完全在多边形内部，因此它是凸的。

At which of the four points above could we position a guard so that the guard would be able to see the entire gallery?
在上述四个点中的哪个位置我们可以布置一名守卫，以便守卫能够看到整个画廊？

A

B

C

D

Explanation 解释

Point B is the only position from which a guard would be able to see the entire gallery. From the other three positions, at least one of the corners of the gallery is blocked from sight by the other walls of the gallery:
点 B 是唯一一个守卫可以看到整个画廊的位置。从其他三个位置，画廊的至少一个角落会被画廊的其他墙壁阻挡，无法看到。

Which of the concave galleries above requires at least two guards — both of whom you can position anywhere in the gallery?
哪个上面的凹形展览馆需要至少两名守卫——你可以将他们中的任何人都放置在展览馆的任何位置？

A

B

C

All three of these galleries require only one guard.
这三个画廊都需要仅一名守卫。

All three of these galleries require at least two guards.
这三个画廊都需要至少两名守卫。

Explanation 解释

Both A and C can be completely guarded by a single guard:
A 和 C 都可以由一个守卫完全保护：

Gallery A can be completely guarded by a guard placed at the center of the star. If we divide gallery C into two rectangles with a vertical line, then a guard placed on this vertical line between the two rectangles would be able to see the entire gallery.
画廊 A 可以通过放置在星形中心的守卫完全守卫。如果我们用一条垂直线将画廊 C 分为两个矩形，那么在两个矩形之间的这条垂直线上放置一个守卫就能看到整个画廊。

Gallery B requires at least two guards to guard completely. If we imagine a cake being placed in the corner with the red dot and a doughnut being placed in the corner with the green dot, then the red and green rectangles represent the areas that have a line of sight to these pastries. Since the rectangles don’t overlap, we need to have at least two guards to properly cover these corners of the gallery.
画廊 B 至少需要两名守卫来完全守卫。如果我们想象一个带有红色点的蛋糕放在角落里，一个甜甜圈放在带有绿色点的角落里，那么红色和绿色的矩形代表可以看到这些糕点的区域。由于矩形不重叠，我们需要至少两名守卫来正确覆盖画廊的这些角落。

You might have noticed that one of the unique properties of concave figures is that some of the internal angles are greater than 180∘.180∘. These angles are called reflex angles.
你可能会注意到，凹形图形的一个独特性质是，其中一些内角大于 0# 这些角度被称为反角。

Consider these two statements:
考虑这两个陈述：

A. Any simple polygon that has an interior reflex angle is concave or non-convex.
A. 任何具有内角为反射角的简单多边形都是凹形或多面形。

B. If a simple polygon has no interior reflex angle, then it’s definitely convex.
B. 如果简单多边形没有内部折角，则它肯定是凸多边形。

Which statement is true? 哪项陈述是真的？

Only A 只有 A

Only B 只有 B

A and B are both true.
A 和 B 都是真的。

A and B are both false.
A 和 B 都是假的。

Explanation 解释

Both statements are true.
两个陈述都是真的。

To see that statement A is true, consider a simple polygon that has an interior reflex angle:
要验证陈述 A 为真，考虑一个具有内角反射的简单多边形：

If we consider two points on the edges that form the reflex angle, the line connecting them must travel outside of the polygon, so it cannot be convex and is instead concave.
如果我们考虑形成反角的两个边端点，连接它们的线必须位于多边形之外，因此它不能是凸的，而是凹的。

We can see that statement B is true by showing how assuming that it’s not true will lead to a contradiction. Let’s assume that we have a shape that has no interior reflex angles but is still concave. We’ll show that if the shape is concave, one of the interior angles must be a reflex angle, which would be a contradiction.
我们可以看出，通过展示假设它不正确会导致矛盾，陈述 B 是真的。让我们假设有一个没有内部反角但仍然是凹形的形状。我们将展示，如果形状是凹形的，那么必须有一个内部角度是反角，这将是一个矛盾。

Since the shape is concave (not convex), we can find two points on the perimeter such that the straight line segment connecting them passes outside of the polygon:
由于形状是凹的（不是凸的），我们可以找到边界上的两个点，使得连接它们的直线段位于多边形之外：

Since the line starts on the perimeter of the polygon, passes outside, and ends up back at the perimeter, we can always find some segment of this line that connects two points on the perimeter and is otherwise entirely outside of the polygon.
由于这条线从多边形的边缘开始，穿过外部，最终又回到边缘，我们总能找到这条线中的一些段，该段连接两个边缘上的点，且除了这条段外，其余部分完全位于多边形之外。

That means that this line — along with at least two of the sides of the polygon — forms a new polygon outside of the one we had. Now, let’s consider the angles of this new polygon we’ve formed outside our polygon. The polygon has some number of sides, n,n, and a total angle sum of 180∘(n−2).180∘(n−2). In order to have the correct angle sum, at least three of the interior angles of any polygon must be less than 180∘.180∘. This is because if all but two of the interior angles of a polygon were 180∘180∘ or greater, their sum would be equal to or greater than 180∘(n−2),180∘(n−2), which would make it impossible to have more angles. Since there are three of these non-reflex angles and our red side only forms two of the angles of our new polygon, at least one of the non-reflex angles is formed by the intersection of two of the sides of our original polygon:
这意味着这一行——以及至少两条多边形的边——形成了一个多边形，这个多边形在我们原有的多边形之外。现在，让我们考虑我们形成的新多边形的角。这个新多边形有 n,n, 条边，总角度和为 180∘(n−2).180∘(n−2). 。为了有正确的角度和，任何多边形的至少三个内角必须小于 180∘.180∘. 。这是因为如果一个多边形除了两个内角之外的所有内角都大于或等于 180∘180∘ ，它们的总和就会等于或大于 180∘(n−2),180∘(n−2), ，这就使得不可能有更多角度。由于有三个这些非反射角，而我们的红色边只形成了我们新多边形的两个角，至少有一个非反射角是由我们原始多边形的两条边的交点形成的。

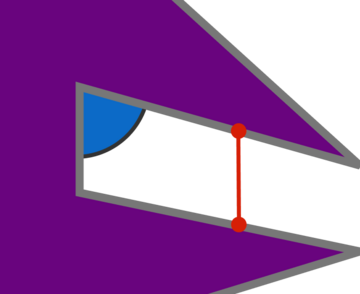
However, this non-reflex angle is also an exterior angle of our original polygon, which means that the sum of this angle and its interior angle pair must be 360∘.360∘. Since the exterior angle measures less than 180∘,180∘, the interior angle must be greater than 180∘:180∘:
然而，这个非反射角度也是我们原始多边形的外角，这意味着这个角度与其内角对的和必须等于 360∘.360∘. 因为外角的度数小于 180∘,180∘, 内角必须大于 180∘:180∘:

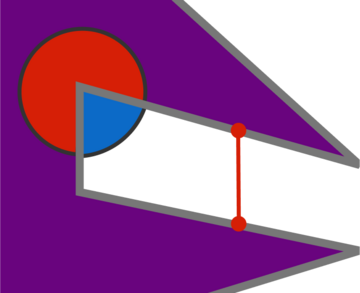
That means we’ve found a reflex angle in our original simple polygon, which is a contradiction.
这意味着我们在原始简单多边形中找到了一个反射角，这是矛盾的。

Which of the three lines drawn on the polygon cuts the polygon into two convex pieces?
在多边形上的哪一条线将多边形切割成两个凸形部分？

A

B

C

All of the lines cut the polygon into two convex pieces.
所有线都将多边形切割成两部分凸形。

Explanation 解释

If a cut is made along either line A or C, one of the pieces created is still concave, since it’s possible to find a line between two points on the perimeter that lies outside the shape. However, a cut across line B does cut the polygon into two convex pieces:
如果沿着 A 线或 C 线进行切割，产生的一个部分仍然可能是凹形的，因为在形状的边缘两点之间能找到一条位于形状外部的线。然而，穿过 B 线的切割会将多边形切成两个凸形部分：

The position of the interior reflex angles can tell us a lot about a polygon. In particular, if an irregular polygon has only two reflex angles, and if the line between those angles dissects both angles into pieces that each measure less than 180∘,180∘, then that line is effectively dissecting the large concave polygon into two convex polygons:
内反射角的位置可以告诉我们很多关于多边形的信息。特别是，如果一个不规则多边形只有两个反射角，并且如果连接这些角度的线将这两个角度分割成每个部分都小于 180∘,180∘, 的片段，那么这条线实际上将这个大的凹多边形分割成两个凸多边形：

Note that in the rightmost image above, the red line connecting the two reflex angles doesn’t dissect the polygon because the two vertices are adjacent. As a result, there’s no way to cut this last polygon into two convex pieces.
请注意，在上方最右边的图片中，连接两个反射角的红色线没有分割多边形，因为两个顶点是相邻的。因此，没有办法将这个最后的多边形切割成两个凸部分。

These observations relate to the museum guard problem in a very direct way that we’ll apply in the next problem.
这些观察与我们将在下一个问题中应用的博物馆警卫问题以非常直接的方式相关。

Which of these galleries cannot be guarded by a single guard?
这些画廊中，哪一个不能由一名守卫守护？

A

B

C

D

They each require only one guard.
他们每个人只需要一个守卫。

Explanation 解释

We know that if a simple polygon is convex, a guard can guard it from anywhere within or on the edge of that shape. Therefore, if a shape is made of two convex shapes connected by an edge, a guard can definitely see all of both areas from any point on that edge.Possible cases: A, B, D
我们知道，如果一个简单多边形是凸的，那么可以从该形状内部或边缘的任何位置对其进行守卫。因此，如果一个形状由两个通过边连接的凸形状组成，那么从该边上的任何一点，守卫都可以看到两个区域的所有部分。可能的情况：A，B，D

Shape A has one reflex angle, so it can be cut into two convex polygons and guarded by one guard. Note that a reflex angle measures less than 360∘,360∘, so cutting it in half will always result in two angles, each less than 180∘.180∘.
形状 A 有一个反角，因此它可以被切割成两个凸多边形，并由一个守卫进行防守。请注意，反角的度数小于 360∘,360∘, ，因此将其二等分总是会得到两个角度，每个角度都小于 180∘.180∘.

Shape B has two reflex angles but it’s possible to draw a line between them that cuts those angles into four non-reflex angles so that the two pieces are convex polygons and the gallery can be guarded by one guard positioned on the dissecting edge.
形状 B 有两个反角，但有可能在它们之间绘制一条线，将这些角度切成四个非反角，使得这两部分都是凸多边形，画廊可以通过定位在切割边上的一个守卫来守卫。

Shape D also has two reflex angles, but they are adjacent, so the line between them would not cut this polygon into two convex parts. In fact, extending that reasoning, it’s actually impossible to cut this gallery into two convex parts. However, one guard is still sufficient to guard the gallery if he/she is positioned carefully:
形状 D 也有两个反射角，但它们是相邻的，因此它们之间的线不会将这个多边形切割成两个凸部分。实际上，如果扩展这个推理，实际上不可能将这个画廊切割成两个凸部分。然而，如果他/她被小心地定位，一个警卫仍然足以守卫画廊：

Impossible case: C 不可能的情况：C

Only Figure C cannot be guarded with just a single guard.
只有图 C 不能仅用一个守卫来保护。

Like Figure D, Figure C is a case where the line between the two reflex angles doesn’t cut the polygon into two convex pieces. However, we know from Figure D that this observation alone isn’t enough to conclude that at least two guards are necessary. Instead, in order to prove that two guards are necessary, we need to use the same kind of reasoning demonstrated in previous problems.
如同图 D，图 C 是一个两个反射角之间的线不会将多边形分为两个凸部分的情况。然而，从图 D 我们知道，仅凭这个观察不足以得出至少需要两个守卫的结论。相反，为了证明至少需要两个守卫，我们需要使用类似于之前问题中展示的推理方式。

Picture a piece of cake in the top left corner and a doughnut in the bottom right corner:
想象一下，右上角有一块蛋糕，左下角有一个甜甜圈

The red and green sections indicate the areas that have lines of sight to the cake and doughnut, respectively. Since those areas don’t overlap, we need at least two guards to make sure both those corners are guarded.
红色和绿色的部分表示可以看到蛋糕和甜甜圈的区域，分别对应各自。由于这些区域不重叠，我们需要至少两个守卫来确保都能守卫到这两个角落。

In summary: 总结：

In this problem, one great guard-positioning strategy is to find an edge that cuts the polygon into two convex parts. In order for a polygon to be convex, it must have no reflex angles, so the reflex angles are the ones that need to be cut. However, the line between two reflex angles — if there are two instead of one — might not be able to cut both angles into non-reflex pieces.
在这个问题中，一个优秀的守卫定位策略是找到一条边，将多边形分为两个凸部分。为了使多边形成为凸形，它必须没有凹角，因此凹角是需要被切割的部分。然而，如果存在两个而不是一个凹角，连接这两个凹角的线可能无法将这两个角都切割成非凹角的部分。

In two cases above, A and B, it’s possible to use a single straight line to cut the given reflex angles into pieces that are all smaller than 180∘.180∘. However, in the other two cases, C and D, such a cut is impossible.
在上述两种情况下，A 和 B，有可能使用一条直线将给定的反射角切割成所有小于 180∘.180∘. 的较小角度。然而，在其他两种情况下，C 和 D，这样的切割是不可能的。

It’s then tempting to conclude that in both of these latter two cases using only one guard should be impossible, but in reality it’s still possible to use only one guard in case D.Altogether, the conclusion has two parts:
然后很容易得出结论，在后两种情况下，只使用一个保护措施是不可能的，但在实际情况中，仅在情况 D 中使用一个保护措施仍然是可能的。总的来说，结论有两部分：

Part 11 is that being able to cut a polygon into two convex pieces is sufficient to show that only one guard is needed.
第 11 部分是，能够将多边形切割成两个凸形部分足以表明只需要一个守卫。

And Part 22 is that if a polygon cannot be cut into two convex pieces, then two guards might be needed in some cases, but in other cases one guard might be sufficient.
并且第 0 部分是，如果一个多边形无法被切割成两个凸形部分，那么在某些情况下可能需要两个守卫，但在其他情况下一个守卫可能就足够了。

True or False? 真假？

Any simple, polygonal gallery that can be dissected, or cut, into two convex shapes can be guarded by a single guard.
任何可以被分解或切割成两个凸形的简单多边形画廊都可以由一个守卫守护。

True 真

False 假

Explanation 解释

The statement is true. 陈述是真的。

Let’s consider any polygonal gallery that can be dissected into two convex shapes:
让我们考虑任何可以被分解为两个凸形的多边形画廊：

You can guard the gallery by placing a single guard anywhere along the line that would be used to dissect the shape into the two convex pieces.
您可以在用于将形状分割成两个凸形部分的线的任何位置放置一名守卫来守护画廊。

When a shape is convex, any line between two points on its perimeter is completely contained within the shape. The guard is on the shared perimeter of both of the newly created convex shapes, so any line between the guard and any point along the perimeter of the gallery is contained entirely within the gallery. This means the guard has an unobstructed view to every point along the perimeter of the gallery, so it’s completely guarded.
当一个形状是凸形时，其边界上任意两点之间的线完全位于该形状内部。守卫位于新创建的两个凸形的共享边界上，因此从守卫到画廊边界上任意一点的线完全位于画廊内部。这意味着守卫可以无遮挡地看到画廊边界上的每一个点，因此画廊完全被守卫覆盖。

Quadrilateral and Pentagonal Galleries

四边形和五边形画廊

So far, we know that a convex gallery can be guarded by one guard no matter where you place them. And, on the other hand, some concave galleries require only one guard if you place that guard correctly, but others can require two or even more guards.
到目前为止，我们知道无论将守卫放置在哪里，凸形画廊都可以由一个守卫守卫。另一方面，一些凹形画廊如果将守卫放置得当，只需要一个守卫就可以守卫，但其他画廊可能需要两个或甚至更多的守卫。

In this lesson, we’re going to begin to examine how the number of sides affects the number of guards needed:
在这节课中，我们将开始探讨边的数量如何影响所需的守卫数量：

All triangular galleries can be guarded by a single guard because all triangles are convex, simple polygons. How about quadrilaterals?
所有三角形画廊都可以由一名守卫守护，因为所有三角形都是凸的简单多边形。那么四边形呢？

Is it possible to design a quadrilateral — that is, 44-sided — gallery that requires two guards?
能否设计一个四边形——也就是说， 44 边形——美术馆，需要两个守卫？

Yes 是

No 不

Explanation 解释

At least one of the two diagonals of any quadrilateral will be fully inside the quadrilateral, dissecting it into two triangles:
任何四边形的两条对角线中至少有一条完全位于四边形内部，将四边形分为两个三角形：

Since triangles are convex, any guard placed along this diagonal will be able to completely guard both triangles, which make up the entire quadrilateral gallery.
由于三角形是凸的，因此沿这条对角线放置的任何守卫都将能够完全守护这两个三角形，这两个三角形构成了整个四边形画廊。

Here’s a proof that such a diagonal always exists.
这是一个证明，始终存在这样的对角线。

The solution above used the fact that any quadrilateral can be cut into two triangles by cutting along a diagonal — a straight line connecting two opposite vertices of the quadrilateral. But in order to know that we can always use this technique, it’s necessary to prove that one of the two diagonals will always fall fully inside.
上述解决方案利用了这样一个事实：任何四边形都可以通过沿对角线切割成两个三角形——连接四边形相对顶点的直线。但是，为了知道我们总能使用这种技术，有必要证明两个对角线中的一个总是完全位于内部。

An algorithm for triangulating any quadrilateral:
任何四边形的三角剖分算法：

Any quadrilateral can be triangulated. Here’s how to do it. Start by naming the vertices A,B,C,A,B,C, and DD going around the perimeter of the quadrilateral. Note that the interior of the quadrilateral is the finite region bounded by this perimeter, and that we’ve proven earlier in this course that the four internal angles of a quadrilateral always sum to 360∘:360∘:
任何四边形都可以三角剖分。这是如何操作的。首先，按照四边形周长的顺序命名顶点 A,B,C,A,B,C, 和 DD 。请注意，四边形的内部是这个周长所限定的有限区域，而且我们在这门课程的早期已经证明，四边形的四个内角总是相加为 360∘:360∘: 。

Consider one of the two diagonals of a quadrilateral AC‾AC and extend it as a line.
考虑四边形 AC‾AC 的一个对角线，并将其延长为一条线。

Case 1.1. If the other two vertices of the quadrilateral, BB and D,D, are on opposite sides of this line, then AC‾AC dissects the quadrilateral into two triangles, △ABC△ABC and △ADC.△ADC. AC‾AC must be inside the quadrilateral because it’s the base of both triangles:
如果四边形的其他两个顶点， BB 和 D,D, ，位于这条线的两侧，那么 AC‾AC 将四边形分割成两个三角形， △ABC△ABC 和 △ADC.△ADC. 。 AC‾AC 必须位于四边形内部，因为它是两个三角形的底边

Case 2.2. If the other two vertices of the quadrilateral, BB and D,D, are on the same side of line AC‾,AC, then the diagonal AC‾AC is not inside the quadrilateral as in the two examples below. Instead, the interior of the quadrilateral is the region between the jointed curve ABCABC and the jointed curve ADC.ADC. These curves cannot cross because if they did, the quadrilateral would not be simple. Since they cannot cross, either point BB is inside △ADC,△ADC, or point DD is inside △ABC.△ABC. In either case, the interior of the quadrilateral must be the finite region between the two jointed curves and, therefore, diagonal BD‾BD must be in the interior of the quadrilateral:
情况 2.2. 如果四边形的其他两个顶点， BB 和 D,D, 在同一直线 AC‾,AC, 的同一侧，则对角线 AC‾AC 不在四边形内部，如下两个示例所示。相反，四边形的内部是连接曲线 ABCABC 和连接曲线 ADC.ADC. 之间的区域。这些曲线不能相交，因为如果它们相交，四边形就不会是简单的。既然它们不能相交，那么点 BB 就在 △ADC,△ADC, 内部或者点 DD 就在 △ABC.△ABC. 内部。在任何情况下，四边形的内部都必须是两个连接曲线之间的有限区域，因此对角线 BD‾BD 必须在四边形的内部：

Additionally, therefore, BD‾BD is the base of the two triangles △BCD△BCD and △BAD△BAD which dissects the quadrilateral.
此外，因此， BD‾BD 是两个三角形 △BCD△BCD 和 △BAD△BAD 的底，这两个三角形分割了四边形。

Triangulated Quadrilaterals
三角形四边形

“Triangulation” is a technique used in previous parts of this course. Since any quadrilateral can be thought of as two triangles, glued together along one side, and triangles can always be guarded by one guard, a museum guard can be positioned anywhere on the edge that both triangles share and see the entire quadrilateral.
“三角测量”是本课程前几部分中使用的一种技术。由于任何四边形都可以被视为两个三角形，通过一条边粘合在一起，而三角形总是可以通过一个警卫来守护，因此，博物馆的警卫可以被安置在两个三角形共享的边上，从而看到整个四边形的全部区域。

Below are four irregular pentagons, each of which has been dissected into triangles. Use these triangles to try and figure out where museum guards need to be placed in order to be able to see the whole of each gallery.
以下是四个不规则五边形，每个都已被切割成三角形。使用这些三角形，尝试找出博物馆保安应放置的位置，以便能够看到每个画廊的全部。

Which gallery requires two guards?
哪个美术馆需要两名保安？

A

B

C

D

None of these galleries require two guards.
这些画廊都不需要两名守卫。

Explanation 解释

In every gallery, all three triangles meet at one point, meaning that one guard can definitely see the entirety of each of the three triangles, and thus the entire pentagon from that point. Note that in some pentagons it’s possible to see the entire pentagon from additional points as well:
在每一个画廊中，所有三个三角形都汇聚于一点，这意味着一个守卫肯定能看到这三个三角形的全部，从而能看到从那个点开始的整个五边形。请注意，在某些五边形中，也有可能从额外的点看到整个五边形。

At which point can a single guard be placed so that he or she is able to see the entire gallery?
在哪个位置可以放置一名守卫，以便他或她能够看到整个画廊？

A

B

C

At any of these points
在这些点中的任何一个

At none of these points
在这些点的任何一个地方

Explanation 解释

The images below show the areas that are visible from points A and C. Each of these points have a line of sight to large portions of the gallery, but not the entire thing:
下方的图片展示了从点 A 和点 C 可以看到的区域。这些点各自可以看到画廊的大片区域，但并非全部。

If we triangulate the gallery, point B is the point where all three triangles intersect, so the guard can see the entirety of each of the three triangles from that point:
如果我们对画廊进行三边测量，点 B 是三个三角形的交点，因此守卫可以从那个点看到这三个三角形的全部

True or False? 真假？

A simple pentagon can have at most one internal reflex angle.
一个简单的五边形最多只能有一个内折角。

True 真

False 假

Explanation 解释

The statement is false. One example of a pentagon with more than one internal reflex angle is this:
这个陈述是错误的。一个五边形，具有超过一个内反射角的例子是这样的：

However, it’s true that a pentagon can have at most two internal reflex angles.
然而，确实五边形最多只能有两个内部折角。

True or False? 真假？

All simple pentagonal galleries — convex or concave — can be guarded by a single guard.
所有简单的五边形画廊——无论是凸形还是凹形——都可以由一名守卫来守护。

True 真

False 假

Explanation 解释

We know that one guard is sufficient for any convex polygon. The three different types of concave pentagons have either
我们知道任何凸多边形只需要一个守卫。三种不同的凹五边形类型要么

• one reflex angle,  一个反射角，

• two reflex angles next to each other, or
  两个反射角相邻，或者

• two reflex angles that are separated by a non-reflex angle.
  两个反射角，它们之间有一个非反射角。

An example of each type of concave pentagon is shown below. Notice that in each case, all three triangles intersect at one point, meaning that a guard placed at that point will be able to see the entirety of each of the three triangles:
每种凹五边形的示例如下所示。请注意，在每种情况下，所有三个三角形都交汇于一点，这意味着在该点放置的守卫将能够看到每个三角形的全部：

Efficient Guard Placement

高效警卫布置

As is typical in mathematics, the answers that we have so far only suggest more questions about the art gallery puzzle.
在数学中典型的是，我们目前得到的答案只会引发更多关于美术馆难题的问题。

So far, we’ve found that all 33-, 44-, and 55-sided galleries can be guarded by a single guard. Is this also the case for 66-sided galleries?
到目前为止，我们发现所有 33 边形、 44 边形和 55 边形的画廊都可以由一个守卫守卫。那么 66 边形的画廊也是这样吗？

If not, how many guards might a very awkwardly shaped 66-sided gallery require?
如果不行，那么一个非常形状奇特的 66 面画廊可能需要多少卫兵？

If you want to design a gallery that requires 22 guards, or 3,3, or 4,4, what does that gallery need to look like?
如果你想设计一个需要 22 名保安的画廊，或者 3,3, 或 4,4, 个，这个画廊需要是什么样子的？

What other questions do you have?
你还有其他问题吗？

In this lesson, we’ll play around with galleries with 66 or more sides, searching for patterns in how they can best be guarded.
在这节课中，我们将探索具有 66 个或更多边的画廊，寻找它们最佳防御模式的模式。

We’ll start with some galleries designed by gluing simple shapes together. This gallery is made of rectangles:
我们将从一些通过粘合简单形状设计的画廊开始。这个画廊由矩形组成：

For this gallery, where can two guards be positioned so that the entire gallery can be seen by the two guards?
对于这个画廊，两个守卫应该分别站在哪里，以便两个守卫都能看到整个画廊？

A and B A 和 B

B and C B 和 C

A and C A 和 C

C and D C 和 D

Explanation 解释

All of the guards can see the entirety of the middle room. The only guard that can see the entirety of the lower room is guard A. The only guard that can see the entirety of the right room is guard C. Therefore, the two guards could be positioned at points A and C:
所有守卫都能看到中室的全部。唯一能看到下室全部的守卫是守卫 A。唯一能看到右室全部的守卫是守卫 C。因此，这两个守卫可以位于 A 和 C 这两个点上。

Each square room in this gallery has an area of 100100 square meters. The corner of one room is placed at the midpoint of the wall of the adjacent room:
这个画廊中的每个正方形房间的面积为 100100 平方米。一个房间的角落位于相邻房间墙壁的中点处：

What area — in square meters — of this gallery cannot be seen by the positioned guard?
这个画廊中，有多少平方米的区域是被定位的守卫看不见的？

2525

5050

7575

100100

The above is a gallery of bovine art. What’s the least number of guards needed to guard this gallery?
以上是一组牛仔艺术作品。要守卫这个画廊，最少需要多少名警卫？

Hint: Start by identifying the reflex angles of the polygon and then carve the polygon up into convex pieces.
提示：首先确定多边形的反射角，然后将多边形分割成凸形部分。

22

33

44

55

Explanation 解释

We can begin by identifying the 1010 reflex angles and then connecting the reflex angles in pairs to dissect the gallery into 66 convex polygons. No more than two polygons touch at any given point. Therefore, a total of three guards are sufficient to guard the gallery, with one along each intersection edge of two polygons:
我们可以首先识别出 1010 个反射角，然后将反射角成对连接，将画廊分割成 66 个凸多边形。任何一点上最多只有两个多边形相交。因此，总共需要三个守卫来守护画廊，分别位于两个多边形交边的每一个交叉点上。

To see that three guards are necessary, imagine a cake placed in one of the top-left corners of the gallery, a doughnut placed in one of the top-right corners, and pizza placed in one of the bottom corners, as shown here:

The red, green, and blue areas indicate the locations that have a line of sight to each of these food items. Since none of the three areas overlap, at least 33 guards are required to guard these three corners.
红色、绿色和蓝色区域表示可以看到这些食物位置的地点。由于这三个区域没有重叠，至少需要 33 名守卫来守护这三个角落。

Which of the two orthogonal galleries above requires more guards?
以上两个正交展览馆中，哪一个需要更多的守卫？

A

B

Explanation 解释

Gallery B requires more guards because gallery A can be guarded by 22 guards while gallery B requires at least 33 guards.
画廊 B 需要更多的保安，因为画廊 A 可以由 22 名保安守护，而画廊 B 至少需要 33 名保安。

To see that gallery A can be guarded with two guards, we can imagine two guards placed at two of the reflex angles that are at the bottom of the gallery:
要看到画廊 A 可以用两个守卫守护，我们可以想象将两个守卫放置在画廊底部的两个反射角处：

To see that gallery B requires at least 33 guards, we can imagine a piece of cake placed in the top-right corner of the leftmost section of the gallery, a doughnut placed in the top-left corner of the rightmost section, and a pizza placed at the very top of the middle of the gallery:
要看到画廊 B 至少需要 33 名警卫，我们可以想象一块蛋糕放在画廊最左边区域的右上角，一个甜甜圈放在最右边区域的左上角，而一个比萨饼则放在画廊正中央的顶部

The red, green, and blue sections in the diagram indicate the areas that have a line of sight to each of these food items. Since none of the three sections overlap each other at all, we need at least 33 guards to completely guard the gallery.
图中的红、绿、蓝部分表示可以直视这些食物的区域。由于这三个部分完全不重叠，我们需要至少 33 名警卫来完全守护画廊。

What’s the least number of guards needed to guard the gallery above?
需要最少多少名警卫来守护上方的画廊？

11

22

33

66

Explanation 解释

A minimum of two guards are needed to guard this gallery.
至少需要两名守卫来守护这个画廊。

To see that two guards are capable of guarding the entire gallery, we can place one guard in the middle of each of the hexagonal sections. Each of these guards can then see all of the six rectangular hallways that extend from the section, so each one can see half the gallery and together they see the entire thing:
要看出两个守卫足以守护整个画廊，我们可以在每个六边形区域的中心放置一个守卫。每个守卫都能看到从该区域延伸出的六个矩形通道，因此每个守卫都能看到画廊的一半，合在一起就能看到整个画廊。

To see that two guards are necessary, we can imagine a piece of cake in the corner of the top-left rectangular hallway and a doughnut in the corner of the top-right rectangular hallway:
为了说明需要两个守卫，我们可以想象在顶部左侧矩形走廊的角落里有一块蛋糕，而在顶部右侧矩形走廊的角落里有一块甜甜圈

The red and green areas indicate the sections that have a line of sight to these corners. Since the two sections don’t overlap, we’ll need at least one guard in each section to guard both locations, so there are at least two guards required.
红色和绿色区域表示可以看到这些角落的部分。由于这两部分没有重叠，我们需要至少一名守卫在每一部分来守护这两个位置，因此至少需要两名守卫。

Let’s take a deeper look at this last solvable.
让我们深入探讨这个最后可解决的部分。

What’s the least number of guards needed to guard this gallery?
这个画廊最少需要多少名警卫？

Instead of “dissecting” the gallery into regular polygons, we can sometimes use the technique of covering a gallery with regular polygons to find an efficient solution:
而不是将画廊分解为正多边形，我们有时可以使用用正多边形覆盖画廊的技术来寻找一个有效解决方案：

We can see that, for each half of the gallery, the central hexagonal room and the three rectangular rooms overlap in the shape of a small hexagon, the yellow hexagon in the middle. A guard placed anywhere in this yellow region will be able to see the entirety of the space in the central hexagon and the three rectangular spaces. From the image, we can see that we need one guard in each yellow hexagon, for a total of two guards.
我们可以看到，对于画廊的每一半，中央的六边形房间和三个矩形房间在形状上重叠成一个小六边形，中间的黄色六边形。在这个黄色区域内的任何地方放置一名守卫，他都能看到中央六边形和三个矩形空间的全部。从图片中我们可以看出，我们需要在每个黄色六边形中放置一名守卫，总共需要两名守卫。

What’s the least number of guards needed to guard the gallery above?
需要最少多少名警卫来守护上方的画廊？

Note: The rectangles have been extended into the room as an aid to solving.
注意：矩形已扩展至房间内作为辅助解题。

1

2✅

3

4

Explanation 解释

Let’s use the same polygon-shading technique that we just examined. This gallery is composed of a hexagon and six rectangles. We know that a guard placed anywhere inside of the hexagon will be able to see the entire hexagon. Three of the rectangles overlap in one triangular region, and the other rectangles overlap in another triangular region. Therefore, if we place a guard in each of the two triangular regions located in the diagram below as red and blue, then the two guards will be able to see the entire art gallery:
让我们使用我们刚刚检查过的相同多边形着色技术。这个画廊由一个六边形和六个矩形组成。我们知道，放置在六边形内的任何位置的警卫都将能够看到整个六边形。三个矩形在一个三角形区域重叠，而其他矩形在另一个三角形区域重叠。因此，如果我们将警卫分别放置在图中红色和蓝色的两个三角形区域中，那么这两个警卫将能够看到整个画廊：

What total area — in square meters — of the orthogonal gallery below can be seen by both of the guards on duty at the same time?
以下的正交画廊的总面积——以平方米为单位——同时可以看到两个在岗警卫的区域是多少？

Note that all three rooms are square-shaped and all wall lengths are either 55 or 1010 meters.
请注意，所有三个房间都是正方形的，所有墙壁的长度要么是 55 米，要么是 1010 米。

200200

225225

250250

300300

Explanation 解释

Each square room has an area of 10×10=10010×10=100 square meters. Therefore, the gallery has a total area of 300300 square meters. Both guards can see the entirety of the middle room. Each guard can see exactly 3443​ of the farthest room.
每个正方形房间的面积为 10×10=10010×10=100 平方米。因此，画廊的总面积为 300300 平方米。两个守卫都能看到中间房间的全部。每个守卫都能看到最远房间的恰好 3443​ 。

In the image below, one guard can see the yellow region, one guard can see the blue region, and the green region represents what they can both see, which is 300−25−25=250300−25−25=250 square meters:
在下面的图片中，一名守卫能看到黄色区域，另一名守卫能看到蓝色区域，绿色区域表示他们都能看到的部分，即 300−25−25=250300−25−25=250 平方米：

Worst-Case Designs 最坏情况设计

So far, we’ve seen that some complex-looking galleries can be guarded by very few guards — even if they are concave and have many sides.
到目前为止，我们已经看到，一些看起来很复杂的画廊实际上只需要很少的守卫来保护——即使它们是凹形的并且有很多边。

In this quiz, the goal will be to design galleries with 66 or more sides that require as many guards as possible:
在这个测验中，目标是设计具有 66 个或更多边的画廊，需要尽可能多的守卫：

Using what you now know about triangulation and how it can be used as a tool to find an efficient way to guard many museums, try to design a hexagonal gallery that requires two guards.
使用您现在对三角测量的了解以及它可以用作寻找有效保护众多博物馆方法的工具，尝试设计一个需要两名警卫的六边形画廊。

True or False? 真假？

All simple, hexagonal galleries can be guarded with a single guard.
所有简单的六边形展览馆都可以用一个守卫来守护。

True 真

False 假

Explanation 解释

It’s possible to make a simple hexagonal gallery that requires more than one guard — we just need to make sure that when the hexagon is triangulated, there isn’t a point where all the triangles meet.
有可能创建一个简单的六边形画廊，需要不止一个守卫——我们只需要确保在六边形被三角形化时，没有任何一点是所有三角形交汇的地方。

The simple hexagonal gallery below is an example of a gallery that requires more than a single guard:
下方的简单六边形画廊是一个需要不止一名保安的画廊示例：

To see that we need more than one guard, we can imagine a piece of cake placed at the end of one of the “spikes” and a doughnut placed at the end of the other:
要看到我们需要不止一个守卫，我们可以想象一块蛋糕放在其中一个“尖刺”的末端，而一个甜甜圈放在另一个末端：

The red and green sections indicate the areas that have a direct line of sight to these corners. Since the two areas don’t overlap, we would need to have at least one guard in each to guard those corners.
红色和绿色的部分表示可以直接看到这些角落的区域。由于这两个区域不重叠，我们需要至少在每个区域放置一个守卫来守护那些角落。

More sides mean that we can design a more complex gallery that requires more guards, but how complex will a gallery need to be in order to require 33 or more guards?
更多侧面意味着我们可以设计一个更复杂的画廊，需要更多的保安，但画廊需要到什么程度的复杂性才会需要 33 或更多的保安？

Pictured above is an irregular 1111-sided gallery, triangulated for your convenience. At least how many guards are required to guard it?
上图展示的是一个不规则的 1111 边形画廊，为了您的方便进行了三角剖分。至少需要多少名守卫来守护它？

2

3

4

5

Explanation 解释

33 guards are required to completely guard this gallery.
33 保安人员需要完全守护这个画廊。

The image below shows that 33 guards are sufficient for guarding the entire gallery:
下方的图片显示， 33 名警卫足以保护整个画廊：

To see that 33 guards are necessary, we can imagine that a piece of cake, a doughnut, and a pizza are placed in three corners of the gallery, as shown here:
为了说明 33 保安是必要的，我们可以想象在画廊的三个角落放置了一块蛋糕、一个甜甜圈和一个比萨饼，如下所示：

The red, green, and blue sections indicate the areas that each have a line of sight to each of the pieces of food. Since the three areas don’t overlap, we must have a different guard in each of them to make sure we cover those corners of the gallery. Therefore, 33 guards are necessary.
红色、绿色和蓝色部分表示各自能看到每块食物的区域。由于这三个区域不重叠，我们必须在每个区域都有一个不同的守卫，以确保覆盖画廊的那些角落。因此，需要 33 个守卫。

Which of the 2121-sided galleries above requires more guards?
哪个上面的 2121 面画廊需要更多的守卫？

A

B

They require the same number of guards.
他们需要相同数量的守卫。

Explanation 解释

Both combs require a total of 77 guards, or one for each tooth:
两把梳子总共需要 77 名守卫，或者一个对应每一根齿

So far, we’ve seen that any gallery with 3,4,3,4, or 55 sides can be guarded by a single, well-positioned guard:
到目前为止，我们看到任何一侧有 3,4,3,4, 或 55 个边的画廊都可以通过一个正确位置的守卫来守护：

We’ve also seen that it’s possible to design a 66-sided gallery that requires two guards. It turns out that if we increase the number of sides to 77 or 8,8, the maximum number of guards that we can require is still only two:
我们还发现，设计一个需要两名守卫的 66 面画廊是可能的。实际上，如果我们把边数增加到 77 或 8,8, ，我们能要求的最大守卫数仍然是只有两名。

It isn’t until we get to 99 sides that we can design a gallery that requires three guards:
直到我们到达 99 边时，我们才能设计一个需要三名警卫的画廊：

In the next few questions, we’ll look at a way to design galleries so that we can increase the number of guards required by increasing the sides, and look for a pattern in how many sides are needed. In the next chapter, we’ll be explaining and generalizing the proof for this phenomenon.
在接下来的几个问题中，我们将探讨一种设计画廊的方法，通过增加边的数量来提高所需警卫的数量，并寻找所需边数的模式。在下一章中，我们将解释并概括这一现象的证明。

This style of gallery is known as a comb. How many edges does a 55-tooth comb have?
这种画廊的风格被称为梳子。一把 55 齿的梳子有多少个齿？

1414

1515

1616

Explanation 解释

Each time we add a tooth, the number of edges increases by 3.3. Therefore, a 55-tooth comb requires 33 more edges than a 44-tooth comb, or 1515 edges. Note that the number of edges is three times the number of teeth:
每次添加一个齿，边的数量增加 3.3. 。因此，一个 55 齿的梳子比一个 44 齿的梳子需要多 33 条边，总共 1515 条边。请注意，边的数量是齿数量的三倍：

How many guards are needed in order to guard this 66-tooth comb gallery?
需要多少名守卫来守护这个 66 齿梳画廊？

33

66

88

1212

Explanation 解释

Each tooth requires an additional guard, for a total of 66 guards:
每颗牙齿都需要额外的防护，总共需要 66 个防护装置：

The previous two problems demonstrate one way to make a gallery so that, for every 33 additional sides in the design, one more guard is needed.
之前的两个问题展示了一种方法，即对于设计中每增加 33 个额外的边，就需要增加一个守卫。

It also turns out that this design strategy creates a worst-case scenario for guard staffing. In other words, it’s not possible to make a gallery any harder to guard.
这也表明，这种设计策略为警卫人员的配置创造了一个最坏的情况。换句话说，不可能让画廊变得更难守护。

This fact isn’t obvious. In 1978,1978, Steve Fisk proved it by using triangulation, coloring, and some very clever logic. The next lesson will prove and explore Fisk’s result.
这个事实并不明显。在 1978,1978, 史蒂夫·菲斯克通过三角测量、着色和一些非常巧妙的逻辑证明了它。下一课将证明并探讨菲斯克的结果。

Fisk’s Coloring Proof 菲斯的着色证明

In this lesson, we’ll prove and explore a result first published by Václav Chvátal in 1975.1975.
在这节课中，我们将证明并探讨由瓦茨拉夫·赫瓦塔尔首先在 1975.1975. 发表的结果

Any gallery with nn sides will require at most ⌊n3⌋⌊3n​⌋ guards.
任何有 nn 边的画廊将需要最多 ⌊n3⌋⌊3n​⌋ 名警卫。

⌊ ⌋⌊ ⌋ is a function called “floor.” It means rounding the number down to the nearest integer, no matter how close it might be to the integer above it.
⌊ ⌋⌊ ⌋ 是一个名为“地板”的函数。这意味着将数字向下舍入到最接近的整数，无论它可能接近上方的整数有多近。

For example, ⌊52⌋=2.⌊25​⌋=2. Now, it’s your turn.
例如， ⌊52⌋=2.⌊25​⌋=2. 现在，该你了。

What is ⌊103⌋?⌊310​⌋?  ⌊103⌋?⌊310​⌋?

3

4

6

7

Explanation 解释

We have 103≈3.33,310​≈3.33, and we’re going to round this result down to the nearest integer, so ⌊103⌋=3.⌊310​⌋=3.
我们有 103≈3.33,310​≈3.33, 并且我们将把这个结果向下舍入到最接近的整数，所以 ⌊103⌋=3.⌊310​⌋=3.

Fisk simplified Chvátal’s proof. The next three problems will take you through Fisk’s proof step by step. The goal is to show where to position ⌊n3⌋⌊3n​⌋ guards to guard a polygon that has nn sides.
菲斯简化了丘瓦塔尔的证明。接下来的三个问题将一步步引导你理解菲斯的证明。目标是展示如何布置 ⌊n3⌋⌊3n​⌋ 个守卫来保卫一个有 nn 边的多边形。

Here’s the polygon we’ll use. Because it has 1313 sides, Fisk’s technique will allow us to find a way to guard it with a maximum of ⌊133⌋=4⌊313​⌋=4 guards.
这是我们将使用的多边形。因为它有 1313 条边，菲斯克的技术将使我们能够用最多 ⌊133⌋=4⌊313​⌋=4 个守卫来保护它。

We’ll be doing all three steps with the polygon above — however, this technique works for any simple polygon.
我们将使用上方的多边形执行所有三个步骤——然而，此技术适用于任何简单的多边形。

Step 1:1: Triangulate the gallery and color the corners of the triangulation with three colors so that every triangle has exactly one vertex of each color.
步骤 1:1: 对画廊进行三角剖分，并用三种颜色给三角剖分的每个角着色，确保每个三角形恰好有一个顶点是每种颜色。

Example: 示例：

The triangulation and coloring of the polygon above have already been started. What color will vertex XX be?
上述多边形的三角剖分和着色已经开始了。顶点 XX 将会是什么颜色？

Red 红

Blue 蓝色

Green 绿

Explanation 解释

Given that each triangle must have one vertex of each color, we can begin on the right side of the figure to color in vertices. On the upper-right side of the figure, a triangle has one blue and one red vertex, so its third vertex must be green. Then, continuing the left, the last vertex in this triangle must be blue. Therefore, vertex XX must be red:
鉴于每个三角形必须有一个每个颜色的顶点，我们可以从图形的右侧开始填充顶点。在图形的上右部，一个三角形有一个蓝色和一个红色的顶点，因此它的第三个顶点必须是绿色。然后，继续向左，这个三角形中的最后一个顶点必须是蓝色。因此，顶点 XX 必须是红色：

Note that proving that triangulation and coloring are always possible is a little tricky. The full proof can be found here — The Art Gallery Problem “https://brilliant.org/wiki/guarding-a-museum/”.
请注意，证明三角剖分和着色总是可能的有些棘手。完整的证明可以在这里找到——“博物馆守卫问题”——“https://brilliant.org/wiki/guarding-a-museum/”。

Step 2:2: Find the color used the least.
步骤 2:2: 找出使用的颜色最少的。

The coloring of the 1313-sided polygon above uses red 55 times, green 44 times, and blue 44 times.
上述 1313 边形的着色使用红色 55 次，绿色 44 次，蓝色 44 次。

True or False? 真假？

For any 1919-sided polygon, the color used the least will be used no more than 55 times.
对于任何 1919 边形，使用的最少颜色将不会超过 55 次。

True 真

False 假

Explanation 解释

Since ⌊193⌋=6,⌊319​⌋=6, there’s actually a worst-case scenario for a 1919-sided polygon in which each color will be used at least 66 times. Or more exactly, two colors will each be used 66 times and one color will be used 77 times.
由于 ⌊193⌋=6,⌊319​⌋=6, ，实际上对于一个 1919 边形来说，存在最坏的情况，其中每种颜色至少会被使用 66 次。或者说更精确地，两种颜色各自会被使用 66 次，而一种颜色会被使用 77 次。

An example of this would be the comb style galleries from the previous chapter, like this one:
这是一个例子，比如上一章中的梳子风格画廊，就像这样的：

If we triangulate and color the vertices of this gallery, we see that we need the 6-6-76-6-7 distribution of dots described:
如果我们对这个画廊的顶点进行三边形划分并着色，我们会发现我们需要以下 6-6-76-6-7 点的分布：

Step 3:3: Position the guards on the vertices of the color least used in the coloring.
步骤 3:3: 将守卫放置在使用最少的颜色的顶点上。

Because each triangle in the triangulation has one vertex of each color, placing a guard on every instance of one color of vertex will necessarily mean that at least one guard can see every triangular region.
由于三明治中的每个三角形都有一个每个颜色的顶点，因此在每个颜色的顶点实例上放置一个守卫必然意味着至少有一个守卫可以看到每个三角形区域。

Following the three steps we’ve just introduced and given the one guard location on the top-left vertex above, which vertex does a guard get placed on?
遵循我们刚刚介绍的三个步骤，并考虑到上方左上角的唯一守卫位置，守卫会被放置在哪个顶点？

• Step 1:1: Triangulate the polygon — which is complete in the picture — and then color its vertices with three colors so that every triangle has one vertex of each color.
  步骤 1:1: 对多边形进行三角剖分——图片中的多边形已经完成——然后用三种颜色给顶点着色，使得每个三角形都有一个每个颜色的顶点。

• Step 2:2: Identify the color used the least.
  步骤 2:2: 确定使用最少的颜色。

• Step 3:3: Position a guard on every vertex of that color.
  在每种颜色的每个顶点放置一个守卫。

AA

BB

CC

Explanation 解释

The given guard is placed on green, so the additional three guards will also be placed on green, including point C.C.
给定的警卫放在绿色上，因此额外的三个警卫也将放在绿色上，包括点 C.C.

Here’s a new gallery to test Fisk’s method on:
这是用于测试 Fisk 方法的新画廊：

Triangulate, color, and position guards on vertices of this polygonal gallery. How many guards do you need?
三角化，着色，并在该多边形画廊的顶点上放置守卫。你需要多少名守卫？

22

33

44

55

Explanation 解释

We have 33 green dots, 33 blue dots, and 44 red dots. Therefore, we could place the guards on either the green or blue dots and would need a total of 33 guards:
我们有 33 个绿色点， 33 个蓝色点，和 44 个红色点。因此，我们可以将守卫放置在绿色或蓝色点上，总共需要 33 个守卫：

Fisk’s proof guarantees that every gallery with ss sides requires at most ⌊s3⌋⌊3s​⌋ guards, and the comb gives us an example of how to construct galleries that require that many guards. However, most galleries don’t require the maximum number of guards, given the number of sides.
菲斯的证明保证了每间有 ss 边的画廊至少需要不超过 ⌊s3⌋⌊3s​⌋ 名警卫，而梳状结构给出了需要如此多警卫的画廊的例子。然而，大多数画廊在给定边数的情况下，并不需要最大数量的警卫。

It is, after all, possible to design a 100100-sided gallery that requires only one guard:
毕竟，设计一个只需要一个警卫的 100100 面画廊是可能的：

What’s the greatest number of guards that a 100100-sided gallery might need?
一个 100100 边的画廊可能需要的最大数量的警卫是多少？

30

33

34

35

Explanation 解释

Any gallery with nn sides will require at most ⌊n3⌋⌊3n​⌋ guards, so a 100100-sided gallery needs at most ⌊1003⌋=33⌊3100​⌋=33 guards.
任何有 nn 边的画廊都需要最多 ⌊n3⌋⌊3n​⌋ 名警卫，因此一个 100100 边的画廊最多需要 ⌊1003⌋=33⌊3100​⌋=33 名警卫。

Further Art Gallery Research

So far, we’ve thoroughly explored one interesting corner of the art gallery problem and looked into Fisk’s proof of one big result — simple polygon art galleries with ss sides require at most ⌊s3⌋⌊3s​⌋ guards.

However, there’s a lot more to this problem that you might enjoy exploring.

This last art-gallery lesson will introduce seven interesting extensions to the museum guard puzzle that you might pursue if you want to keep investigating this problem:

Internal walls:

How many guards are needed to guard this gallery?

Note: Guards cannot see through internal walls, just as they cannot see through external walls. However, we can assume that the internal walls have negligible thickness.

1

2

3

4

Why?

Explanation

Three guards are needed to guard this gallery.

To see that three guards are sufficient to guard the gallery, we can imagine a guard placement like the one below. Since the walls have negligible thickness, a guard positioned in line with the partial internal walls will be able to see on both sides of it:

To see that three guards are necessary, we can imagine a piece of cake, a doughnut, and a pizza placed in three corners of the gallery, as shown here:

The red, green, and blue regions represent the areas that each have a line of sight to the corresponding food item. Since these areas don’t overlap, at least one guard is required in each, so at least three guards are necessary to guard this gallery.

Internal gardens:

Polygons don’t have holes, but what if we want one in our gallery? Here are some gallery floor plans that have holes:

Mathematically, a hole is created by drawing a simple polygon inside of a standard gallery without intersecting any of the gallery walls. The gallery is then redefined as the region within the larger polygon but not within the smaller polygon or polygons.

True or False?

Any gallery with a hole will require at least two guards.

True

False

Why?

Explanation

It’s true that any gallery with a hole will require at least two guards.

We can see that it’s true by showing that one guard can never guard the gallery by himself.

If we have a gallery with a hole, we can consider a point — shown in green — inside the gallery that is just next to the side of the hole. If we want a single guard to see the gallery, he’ll have to be positioned so that he has a line of sight to this point:

However, if we imagine extending that line of sight through the hole, it must pass out at the other side of the hole to another point inside the gallery shown in red. This is because the boundary of the hole can’t touch any part of the boundary of the gallery — otherwise, it would be part of the gallery wall and not a hole. The guard will not be able to see this second point, so he can’t see the entire gallery:

It is worth noting that this second point can’t be found if the guard is placed in line with the wall of the hole. However, a guard can’t be placed in line with all the walls of a hole at once, so if this is the case, the process can be repeated with another wall to find a point that isn’t visible to the guard.

Orthogonal galleries:

As defined in the first lesson, orthogonal polygons are polygons in which every internal angle measures either exactly 90∘90∘ or exactly 270∘:270∘:

Orthogonal galleries obey special rules. What’s the least number of guards needed to guard this 1616-sided gallery?

3

4

5

6

Why?

Explanation

Four guards are needed to guard this 1616-sided gallery.

To see that four guards are sufficient, we can picture them placed as they are in this image:

To see that four guards are necessary, we can picture a pizza, a piece of cake, a doughnut, and a piece of chocolate placed as shown below, with each placed in one of the right angles:

The blue, red, green, and brown sections represent the areas that have a line of sight to each of these food items. Since none of the four areas overlap, we must have at least one guard in each to guard all of these corners of the gallery, so four guards are necessary.

Creating a private office in the middle of a gallery:

Is it possible to place guards in this gallery so that all of the walls are visible to at least one guard but there’s a region in the middle of the polygon that isn’t visible to any guard?

Yes

No

Why?

Explanation

Using the polygon shading method, we see that none of the three guards placed at far ends of the triangular wings of the gallery can see the purple triangle in the middle:

One-way glass gallery:

This puzzle variant is a little creepy. Imagine that all of the walls of a museum are made out of one-way glass so that they look like normal walls to museum patrons inside the museum but guards positioned outside of the museum can look into the museum through those walls.

Note that this isn’t the same as the guards having super-vision. For example, in the image below, the guard is unable to see point A because although he can look through the orange wall into the gallery, he cannot see through the blue wall because the one-way glass doesn’t let you see through the wall in that direction:

Which point in the museum above is visible to exactly two of the guards?

A

B

C

None of the above points are visible to exactly two guards.

Why?

Explanation

Points A and C are visible to all three guards. Only point B is visible to exactly two guards:

Mobile guards:

If two guards walk back and forth along the paths — the dotted lines — above, which point in the gallery will they never be able to see?

A

B

C

They’ll be able to see each of the points.

Why?

Explanation

The guards will be able to see points A and B, but not C.

The diagram below shows possible positions along their paths from which the guards can see points A and B:

To see why they will never be able to see point C, let’s consider the area of the gallery that has a direct line of sight to point C, which is shaded in red below:

Since this area doesn’t intersect the path of either guard, neither one will be able to see point C.

Shortest path of a single guard:

Which of these paths provides the shortest possible distance for the guard who walks along it to see the entire museum?

A

B

C

Why?

Explanation

Path B provides the shortest path for a guard to see the entire museum.

Path A doesn’t work because it doesn’t allow a guard to see the entire museum. If we imagine a piece of cake placed in the top corner of the museum, the red region indicates the area that has a line of sight to that piece of cake. Since the path doesn’t cross the red area, the guard wouldn’t be able to see that corner of the museum:

Both path B and path C allow the guard to see the entire museum. We can show this is true by dividing the museum into convex shapes, as shown here:

Since paths B and C both cross the perimeter of each of the convex shapes that make up the museum, they allow a guard to see the entire museum.

Of those two, path B is the shortest. Both paths cross through the same four points, shown in red below:

Path B crosses through those points in three straight lines, which is the shortest possible distance to do so since no three points are co-linear. Path C, on the other hand, adds two new vertices — the ones shown in black — to that path, which extend the length of the path. Path B is the shortest path that allows a guard to see the entire museum.

Pegboard Rectangles 钉板矩形

A lattice polygon is one where all the vertices of the polygon coincide with points on a regular grid:
晶格多边形 是多边形的所有顶点与规则网格上的点重合的多边形：

Our ultimate goal is to find the area of lattice polygons like the one above. While it’s possible to break the figures apart and use the area formula for rectangles
我们的最终目标是找到上面那个晶格多边形的面积。虽然可以将数字分开并对矩形使用面积公式

length×widthlength×width

and that for triangles  而三角形的

12×base×height21​×base×height

to work out each area individually, and add the areas together:
要单独计算每个区域，并将这些区域一起添加：

3+1+1.5+0.5+0.75+0.25=7 square units.3+1+1.5+0.5+0.75+0.25=7 square units.

But there’s a much quicker approach, using something called Pick’s theorem.
但是有一种更快的方法，使用一种叫做 Pick 定理的方法。

To get to Pick’s theorem, we’ll need some terminology first.
要获得 Pick 定理，我们首先需要一些术语。

A boundary point is a point on the lattice that coincides with a side or vertex of a polygon. The total number of boundary points of a polygon is written as B.B.
边界点是晶格上与多边形的边或顶点重合的点。多边形的边界点总数写为 B.B.

An interior point is a point on a lattice that is contained within a polygon. The total number of interior points of a polygon is written as I.I.
内部点 是格子上包含在多边形内的点。多边形的内部点总数写为 I.I.

   How many boundary and interior points are on the figure above?
上图中有多少个边界点和内部点？

B=12,I=12B=12,I=12

B=16,I=8B=16,I=8

B=16,I=12B=16,I=12

B=20,I=8B=20,I=8

B=20,I=12B=20,I=12

Explanation 解释

On the boundary, we have 44 points on top, 44 on bottom, and 44 on each side — don’t overcount the corners — for a total of 4+4+4+4=164+4+4+4=16 boundary points.
在边界上，我们在顶部有 44 点， 底部有 44 ，每侧有 44 点 — 不要多计算角 — 总共有 4+4+4+4=164+4+4+4=16 边界点。

We also have 2⋅4=82⋅4=8 interior points.
我们也有 2⋅4=82⋅4=8 内部点。

Given a rectangle with xx dots on two sides and yy dots on the other two, how many boundary points BB does it have?
给定一个矩形 ，两侧有 xx 点，另外两条边有 yy 点，它有多少个边界点 BB ？

B=2x+2yB=2x+2y

B=x2+y2B=x2+y2

B=2x+2y−2B=2x+2y−2

B=x2+y2−2B=x2+y2−2

B=2x+2y−4B=2x+2y−4

B=x2+y2−4B=x2+y2−4

Explanation 解释

xx will occur once each on opposite sides of the rectangle, as will y,y, resulting in x+x+y+y=2x+2y.x+x+y+y=2x+2y. However, there’s overcounting going on, because each of the four corners is counted twice. Therefore, we need to subtract 44 to compensate, and the number of boundary points is 2x+2y−4.2x+2y−4.
xx 将在矩形的相对两侧各出现一次，@1# 也会出现，从而导致 x+x+y+y=2x+2y.x+x+y+y=2x+2y. 但是，存在过度计数的情况，因为四个角中的每一个都被计算了两次。所以我们需要减去 44 来补偿，边界点的数量是 2x+2y−4.2x+2y−4.

Given a rectangle with xx dots on two sides and yy dots on the other two, how many interior points II does it have?
给定一个矩形 ，两侧有 xx 点，另外两条边有 yy 点，它有多少个内部点 II ？

(2x−1)(2y−1)−4(2x−1)(2y−1)−4

(2x−1)(2y−1)(2x−1)(2y−1)

(x−2)(y−2)−4(x−2)(y−2)−4

(x−2)(y−2)(x−2)(y−2)

Explanation 解释

The interior is a rectangle with dimensions (x−2)(x−2) by (y−2),(y−2), that is, the dimensions of the rectangle with each end snipped off.
内部是一个尺寸为 (x−2)(x−2) 乘以 (y−2),(y−2), 的矩形，即矩形的尺寸，两端都被剪掉。

II then consists of all of the points in this interior rectangle, that is, the area (x−2)(y−2).(x−2)(y−2).
II 则由这个内部矩形中的所有点组成，即区域 (x−2)(y−2).(x−2)(y−2).

Let’s generate the area of the rectangle out of the boundary points BB and interior points I.I.
让我们在边界点 BB 和内部点 I.I. 之外生成矩形的面积

Suppose each interior point — marked purple — is the upper-left corner of a unit square, as shown above. We want to fill the remainder of the rectangle with unit squares in the same way, using the boundary points. How many boundary points will be needed?
假设每个内部点 （ 标记为紫色 ） 都是单位正方形的左上角，如上所示。我们想用相同的方式，使用边界点用单位方块填充矩形的其余部分。需要多少个边界点？

B4−14B​−1

B4−44B​−4

B2−12B​−1

B2−42B​−4

Explanation 解释

Half the boundary points are marked on the diagram above. If each is used as the upper-left corner of a unit square, the entire rectangle is filled except there’s one extra unit square.
上图中标记了一半的边界点。如果每个都用作单位正方形的左上角，则整个矩形将被填充，但有一个额外的单位正方形除外。

Therefore, the number of boundary points needed is B2−1.2B​−1. Note that the −1−1 is there to remove the extra unit square.
因此，所需的边界点数为 B2−1.2B​−1. 请注意， −1−1 用于删除额外的单位平方。

Applying the knowledge from the previous question, we now can write Pick’s theorem for rectangles.
应用上一个问题中的知识，我们现在可以写矩形的 Pick 定理。

Given a lattice rectangle with BB boundary points and II interior points, the area of the polygon is ..
给定一个边界点为 BB 且内部点为 II 的格子矩形，则多边形的面积为 ..

B2+I4−42B​+4I​−4

B2+I4−12B​+4I​−1

B2+I−42B​+I−4

B2+I−12B​+I−1

Explanation 解释

We simply want the interior points II to be added to the formula B2−12B​−1 from the previous question, as each one represents the upper-left corner of a unit square filling the whole rectangle. That is, we need B2+I−1.2B​+I−1.
我们只想将内部点 II 添加到上一个问题的公式 B2−12B​−1 中，因为每个点都代表填充整个矩形的单位正方形的左上角。也就是说，我们需要 B2+I−1.2B​+I−1.

Justify Any Configuration of Unit Squares — Part 11
证明任何单位平方的配置— 第 11 部分

We now want to justify our formula for any configuration of unit squares glued together, no matter how irregular:
我们现在想要证明我们的公式对于粘合在一起的任何单位平方的配置，无论多么不规则：

Since we know the formula B2+I−12B​+I−1 will work for any arbitrary rectangle, we can start with a rectangle. Then, if we can show that adding a unit square anywhere — increasing the area by 11 — causes a change in boundary and interior points so that B2+I−12B​+I−1 increases by 1,1, we will know the formula works for any configuration of unit squares glued into a single polygon.
由于我们知道公式 B2+I−12B​+I−1 适用于任何任意矩形，因此我们可以从一个矩形开始。然后，如果我们能证明在任何地方添加一个单位正方形 —— 将面积增加 11 —— 会导致边界和内部点发生变化，因此 B2+I−12B​+I−1 增加 1,1, ，我们就会知道该公式适用于粘在单个多边形中的单位正方形的任何配置。

Justify Any Configuration of Unit Squares — Part 22
证明任何单位平方的配置— 第 22 部分

A unit square can be added to touch one side, two sides, or three sides, as shown above. Four sides would require a “hole,” which by definition wouldn’t result in a polygon.
可以添加单位正方形以接触一侧、两侧或三侧，如上所示。四条边需要一个 “hole”，根据定义，这不会产生多边形。

When the unit square touches one side, the effect is to add 22 boundary points. This adds 11 to the expression B2+I−1:2B​+I−1:
当单位正方形接触一侧时，效果是添加 22 边界点。这会将 11 添加到表达式 B2+I−1:2B​+I−1: 中

B+22+I−1=B2+22+I−1=B2+1+I−1=(B2+I−1)+1,2B+2​+I−1​=2B​+22​+I−1=2B​+1+I−1=(2B​+I−1)+1,​

which is consistent with adding 11 to the area.
这与将 11 添加到该区域一致。

What’s the effect of adding a unit square that touches two existing sides as in the figure above?
如上图所示，添加一个接触两个现有边的单位正方形会产生什么影响？

11 subtracted from boundary points, 11 added to interior points
11 从边界点中减去， 11 添加到内部点

No change in boundary points, 11 added to interior points
边界点没有变化， 11 添加到内部点

No change in boundary points, 22 added to interior points
边界点没有变化， 22 添加到内部点

11 added to boundary points, no change in interior points
11 添加到边界点，内部点没有变化

11 added to boundary points, 11 added to interior points
11 已添加到边界点， 11 已添加到内部点

Justify Any Configuration of Unit Squares — Part 33
证明任何单位平方的配置— 第 33 部分

Combining this answer with the one from the last question, you’ll have justified that Pick’s theorem is stable when adding unit squares onto a figure, which means it applies to any configuration of unit squares at all. This approach will be useful later when we prove Pick’s theorem works for all lattice polygons, not just ones made out of squares.
将这个答案与上一个问题的答案结合起来，您将证明当将单位平方添加到图形上时，Pick 定理是稳定的，这意味着它完全适用于 任何 单位平方的配置。当我们稍后证明 Pick 定理适用于所有晶格多边形时，这种方法将非常有用，而不仅仅是由正方形组成的多边形。

What’s the effect of adding a unit square that touches three existing sides?
添加一个触及三个现有边的单位正方形有什么效果？

22 subtracted from boundary points, 22 added to interior points
22 从边界点中减去， 22 添加到内部点

22 subtracted from boundary points, no change in interior points
22 从边界点中减去，内部点没有变化

11 subtracted from boundary points, 22 added to interior points
11 从边界点中减去， 22 添加到内部点

No change in boundary points, 22 added to interior points
边界点没有变化， 22 添加到内部点

11 added to boundary points, 11 added to interior points 重试  错误原因

Why? 

Explanation 解释

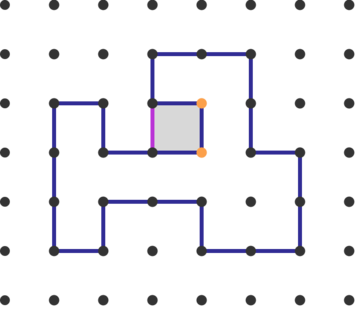
The two orange points turn from boundary points into interior points, so boundary points decrease by 22 and interior points increase by 2.2.
两个橙色点从边界点变为内部点，因此边界点减少 22 ，内部点增加 2.2.

The effect on B2+I−12B​+I−1 is again, as hoped, to increase by 1:1:
正如所希望的那样，对 B2+I−12B​+I−1 的影响再次增加 1:1:

B−22+(I+2)−1=B2−22+I+2−1=B2−1+I+2−1=(B2+I−1)+1.2B−2​+(I+2)−1​=2B​−22​+I+2−1=2B​−1+I+2−1=(2B​+I−1)+1.​

Since all three cases are accounted for, any lattice polygon made by gluing together unit squares will have an area given by B2+I−1.2B​+I−1.
由于考虑了所有三种情况，因此通过将单位方块粘合在一起而形成的任何晶格多边形都将具有由 B2+I−1.2B​+I−1. 给出的面积

Pick’s Theorem Generalized

In the last lesson, we showed that Pick’s theorem — that the area of figure is B2+I−1,2B​+I−1, where BB is the number of boundary points and II is the number of interior points — applies to any triangle:
在上一课中，我们展示了 Pick 定理 — 图形的面积是 B2+I−1,2B​+I−1, ，其中 BB 是边界点的数量， II 是内部点的数量 — 适用于任何三角形：

Now we want to apply the theorem to any lattice polygon whatsoever. This is possible because of what you learned in the art gallery puzzle about triangulation — that any irregular polygon can be cut into triangles using the vertices of the original polygon as vertices of the triangles.
现在我们想将定理应用于任何晶格多边形。这是可能的，因为你在 art gallery 谜题中学到了关于三角剖分的知识 — 任何不规则的多边形都可以使用原始多边形的顶点作为三角形的顶点来切割成三角形。

For example, what’s the minimum number of triangles required to triangulate the figure above?
例如，对上图进行三角剖分所需的最小三角形数是多少？

5

6

7

8

9

Consider two lattice polygons being attached — one with BB boundary points and II interior points, and the other with CC boundary points and JJ interior points:
考虑附加的两个晶格多边形 — 一个带有 BB 边界点和 II 内部点，另一个带有 CC 边界点和 JJ 内部点：

If Pick’s theorem holds, what will the overall area of the combined figure be?
如果皮克定理成立，那么组合图的总面积是多少？

B+C2+(I+J)−12B+C​+(I+J)−1

B+C2+(I+J)−22B+C​+(I+J)−2

B+C4+(I+J)−14B+C​+(I+J)−1

B+C4+(I+J)−24B+C​+(I+J)−2

The last question gave the formula expected from merging two lattice polygons — supposing that Pick’s theorem works. We just need to justify this formula will occur no matter the shape of the boundary.
最后一个问题给出了合并两个晶格多边形的预期公式 — 假设 Pick 定理有效。我们只需要证明这个公式无论边界的形状如何都会发生。

Two lattice polygons, when glued together, will always meet at a “path,” as shown above, where the start and end of the path are marked in red and the points inside the path are marked green.
两个晶格多边形在粘合在一起时，将始终在“路径”处相遇，如上所示，其中路径的起点和终点标记为红色，路径内的点标记为绿色。

Considering just the red points, what happens to the sum of boundary points of the two polygons versus the boundary points of the new-merged polygon?
仅考虑红点，两个面的边界点之和与新合并的面的边界点之和会发生什么变化？

The number of boundary points is reduced by 2.2.
边界点的数量减少了 2.2.

The number of boundary points is reduced by 1,1, and interior points reduced by 1.1.
边界点的数量减少了 1,1, ，内部点的数量减少了 1.1.

The number of boundary points is reduced by 2,2, and interior points increased by 1.1.
边界点的数量减少了 2,2, ，内部点的数量增加了 1.1.

Continuing with the same diagram as the last question:
继续上一个问题的相同图表：

Considering just the green points, what’s true?
仅考虑绿点，什么是真的？

For every 22 boundary points on the original polygons, the merged polygon has ..
对于原始多边形上的每个 22 边界点，合并后的多边形具有 ..

11 less boundary point and 11 more interior point
11 少一点边界点和 11 多一点内部点

11 less boundary point and 22 more interior points
11 更少的边界点和 22 更多的内部点

22 less boundary points and 11 more interior point
22 更少的边界点和 11 更多的内部点

22 less boundary points and 22 more interior points
22 更少的边界点和 22 更多的内部点

Merging two lattice polygons, suppose the polygons have BB and CC boundary points and II and JJ interior points, respectively. Also suppose the merged polygon has DD boundary points and KK interior points. Then we want to justify the sum of the areas from the individual polygons B+C2+(I+J)−22B+C​+(I+J)−2 is equal to the result from applying Pick’s theorem to the new polygon, D2+K−1.2D​+K−1.
合并两个晶格多边形，假设多边形分别具有 BB 和 CC 边界点以及 II 和 JJ 内部点。此外，假设合并的多边形具有 DD 边界点和 KK 内部点。然后我们要证明来自各个多边形 B+C2+(I+J)−22B+C​+(I+J)−2 的面积之和等于将 Pick 定理应用于新多边形 D2+K−1.2D​+K−1. 的结果

We’ve concluded two things happen upon merging:
我们得出结论，合并时会发生两种情况：

1. The boundary points sum B+CB+C is reduced by 2.2.
   边界点总和 B+CB+C 减去 2.2.

2. If the path has PP points in the interior, the boundary points sum B+CB+C is reduced by 2P2P and the interior points sum I+JI+J increases by P.P.
   如果路径内部有 PP 点，则边界点总和 B+CB+C 减少 2P2P ，内部点总和 I+JI+J 增加 P.P.

That means D=B+C−2−2PD=B+C−2−2P and K=I+J+P.K=I+J+P.
这意味着 D=B+C−2−2PD=B+C−2−2P 和 K=I+J+P.K=I+J+P.

Substituting gives 代入得到

D2+K−1=B+C−2−2P2+I+J+P−1=B+C2−22−2P2+I+J+P−1=B+C2−1−P+I+J+P−1=B+C2+I+J−2.2D​+K−1​=2B+C−2−2P​+I+J+P−1=2B+C​−22​−22P​+I+J+P−1=2B+C​−1−P+I+J+P−1=2B+C​+I+J−2.​

Thus D2+K−1,2D​+K−1, the result of applying Pick’s theorem to the merged polygon, is equivalent to the sum of areas of the original polygons: B+C2+(I+J)−2.2B+C​+(I+J)−2.
因此 D2+K−1,2D​+K−1, 将 Pick 定理应用于合并多边形的结果，等于原始多边形的面积之和： B+C2+(I+J)−2.2B+C​+(I+J)−2.

This means any irregular lattice polygons whatsoever may be merged and Pick’s theorem still holds. Additionally, since every lattice polygon can be triangulated and Pick’s theorem works on any triangle, Pick’s theorem holds for any irregular polygon.
这意味着任何不规则的晶格多边形都可以合并，并且 Pick 定理仍然成立。此外，由于每个晶格多边形都可以进行三角化，并且 Pick 定理适用于任何三角形，因此 Pick 定理适用于任何不规则多边形。

Let’s try it out on some crazy ones.
让我们在一些疯狂的 图形试试看。

What’s the area of the figure?
图的面积是多少？

1414 square units
1414 平方单位

14.514.5 square units
14.514.5 平方单位

1515 square units
1515 平方单位

15.515.5 square units
15.515.5 平方单位

Explanation 解释

The figure consists of a 55 by 66 grid where every point is a boundary point, plus 11 extra, so there are 5×6+1=315×6+1=31 boundary points and no interior points. By the formula, this has an area of
该图由一个 55 x 66 网格组成，其中每个点都是一个边界点，加上 11 extra，因此有 5×6+1=315×6+1=31 边界点，没有内部点。根据公式，它的面积为

312+0−1=15.5−1=14.5.231​+0−1​=15.5−1=14.5.​

Which has a larger area, figure A or figure B?
图 A 和图 B 哪个面积更大？

A

B

They both have the same area.
它们具有相同的面积。

Explanation 解释

While this is solvable by counting, it’s quicker to note the two figures have identical number of boundary points and interior points except B has 22 less boundary points and 11 more interior point than A.
虽然这可以通过计数来解决，但可以更快地注意到这两个数字具有相同数量的边界点和内部点，除了 B 的 边界点 22 比 A 少 @1# 。

Intuitively, since boundary points are divided by 22 in the expressions of Pick’s formula and interior points are not, 22 boundary points for 11 interior point is an equal trade.
直观地说，由于在 Pick 公式的表达式中边界点被 22 除以，而内部点不是，因此 11 内部点的 22 边界点 是平等的。

More algebraically, if A has XX boundary points and YY interior points, then A has an area of X2+Y−12X​+Y−1 and B has an area of (X−2)2+(Y+1)−1.2(X−2)​+(Y+1)−1. But the two expressions are the same:
更代数地说，如果 A 有 XX 边界点和 YY 内部点，那么 A 的面积是 X2+Y−12X​+Y−1 ， B 的面积是 (X−2)2+(Y+1)−1.2(X−2)​+(Y+1)−1. 但是这两个表达式是相同的：

X−22+Y+1−1=X2−22+1+Y−1=X2+Y−1.2X−2​+Y+1−1​=2X​−22​+1+Y−1=2X​+Y−1.​

Which of these cannot be the area of a lattice polygon?
其中哪一个 不能 是晶格多边形的面积？

10.510.5

113113

200.25200.25

30405.530405.5

All of these are possible.
所有这些都是可能的。

Explanation 解释

The formula B2+I−12B​+I−1 consists of two parts:
公式 B2+I−12B​+I−1 由两部分组成：

• an integer, the I−1I−1 part, and
  一个整数、 I−1I−1 部分和

• an integer divided by 2,2, which is B2.2B​.
  一个整数除以 2,2, ，即 B2.2B​.

While halves are possible with B2,2B​, it cannot possibly make quarters, so 200.25,200.25, or 20014,20041​, is not possible as the area of a lattice polygon.
虽然 B2,2B​, 可以进行一半，但它不可能构成四分之一，因此 200.25,200.25, 或 20014,20041​, 不可能作为晶格多边形的面积。

What’s the area inside the outer figure, excluding the orange portion?
除了橙色部分之外，外部图内部的区域是多少？

1313

13.513.5

1414

14.514.5

1515

15.515.5

Explanation 解释

The most straightforward approach is to do each area individually with Pick’s.
最直接的方法是使用 Pick’s 单独处理每个区域。

In that case, the larger figure has 1414 boundary points and 1111 interior points, for an area of 142+11−1=17.214​+11−1=17. The orange portion has 99 boundary points and 00 interior points, for an area of 92+0−1=3.5.29​+0−1=3.5. Subtracting the orange portion from the larger area gets 17−3.5=13.5.17−3.5=13.5.
在这种情况下，较大的数字有 1414 边界点和 1111 内部点，对于 142+11−1=17.214​+11−1=17. 的区域，橙色部分有 99 边界点和 00 内部点，对于面积 92+0−1=3.5.29​+0−1=3.5. 从较大的区域减去橙色部分得到 17−3.5=13.5.17−3.5=13.5.

Bonus: There’s a way to think of the figure as a whole, including the orange portion as boundary points, and get a version of Pick’s formula that allows for holes.
奖励： 有一种方法可以将图形视为一个整体，包括橙色部分作为边界点，并获得允许孔的 Pick 公式版本。

Keep exploring! 继续探索！

Pick’s Theorem with One Hole

带一个孔的 Pick’s Theorem

At the end of the previous lesson, there was a polygon with a hole inside, where we wanted to find the area excluding the hole:
在上一课的结尾，有一个内部有洞的多边形，我们想在其中找到不包括洞的区域：

One way to manage this problem would be to simply use Pick’s theorem twice and then subtract the results. However, we can take our B2+I−12B​+I−1 and generalize it so that we still only count boundary and interior points on the figure we’re using (without counting holes separately), and we can include any number of holes we want.
解决这个问题的一种方法是简单地使用 Pick 定理两次，然后减去结果。但是，我们可以获取 B2+I−12B​+I−1 并对其进行泛化，以便我们仍然只计算我们正在使用的图形上的边界点和内部点（无需单独计算孔），并且我们可以包含 我们想要的任意数量的孔。

To start with, let’s use one hole only.
首先，我们只使用一个孔。

For now, we’re focusing on problems with just one hole. We’re going to keep track of the original polygon’s boundary points BB and interior points II as if the hole wasn’t there. We’ll also give the number of boundary points B∗B∗ and interior points I∗I∗ of the hole itself.
目前，我们只关注一个球洞的问题。我们将跟踪原始多边形的边界点 BB 和内部点 II ，就好像洞不存在一样。我们还将给出 孔本身的边界点 B∗B∗ 和内部点 I∗I∗ 的数量。

We’ll also consider the combined polygon with the hole, where the points on the outside of the hole are now considered boundary points of the combined polygon. We’ll let QQ be the number of boundary points and RR be the number of interior points — check the example above to see how the counting works.
我们还将考虑带有孔的组合多边形，其中孔外侧的点现在被视为组合多边形的边界点。我们让 QQ 是边界点的数量， 让 RR 是内部点的数量 — 查看上面的示例以了解计数是如何工作的。

What are QQ and RR in the example above?
上面示例中的 QQ 和 RR 是什么？

Note that we don’t have to count the dots one by one.
请注意，我们不必逐个计算点。

Q=14,R=3Q=14,R=3

Q=14,R=4Q=14,R=4

Q=24,R=3Q=24,R=3

Q=24,R=4Q=24,R=4

Explanation 解释

Note that any boundary points B∗B∗ of the hole now become boundary points of the combined polygon, and we add those to the already existing boundary points B.B. So
请注意，孔的任何边界点 B∗B∗ 现在都成为组合多边形的边界点，我们将这些边界点添加到已经存在的边界点 B.B. 中，因此

Q=B+B∗=14+10=24.Q​=B+B∗=14+10=24.​

The interior points of the combined polygon are now reduced: every boundary point and interior point from the hole must be subtracted from the combined polygon’s interior point total. That is, we want
现在，组合多边形的内部点已减少：孔中的每个边界点和内部点都必须从组合多边形的内部点总数中减去。也就是说，我们希望

R=I−B∗−I∗=14−10−1=3.R​=I−B∗−I∗=14−10−1=3.​

So Q=24Q=24 and R=3:R=3:
所以 Q=24Q=24 和 R=3:R=3:

We got two formulas from the answer to the last problem:
我们从最后一个问题的答案中得到了两个公式：

Any boundary points B∗B∗ of the hole now become boundary points of the combined polygon, and we add those to the already existing boundary points B,B, so
洞的任何边界点 B∗B∗ 现在都成为组合多边形的边界点，我们将这些边界点添加到已经存在的边界点 B,B, 中，这样

Q=B+B∗.Q=B+B∗.

Every boundary point and interior point from the hole must be subtracted from the original polygon’s interior count to get the combined polygon’s interior count. That is,
必须从原始多边形的内部计数中减去孔中的每个边界点和内部点，才能得到组合多边形的内部计数。那是

R=I−B∗−I∗.R=I−B∗−I∗.

Now we can combine these together with the original Pick’s formula to get a version of Pick’s in terms of QQ and R.R.
现在我们可以将这些与原始 Pick 的公式组合在一起，以获得 QQ 和 R.R. 的 Pick 版本

Let’s go back to the “slow method” of solving this. Writing it generally, let’s figure out the area of the outer polygon with Pick’s and that of the hole with Pick’s, and subtract the two numbers:
让我们回到解决这个问题的 “慢方法”。 一般来说，让我们用 Pick 计算出外多边形的面积，用 Pick 计算出孔的面积，然后减去这两个数字：

• outer polygon’s area: B2+I−12B​+I−1
  外多边形的面积： B2+I−12B​+I−1

• inner hole’s area: B∗2+I∗−1.2B∗​+I∗−1.
  内孔面积： B∗2+I∗−1.2B∗​+I∗−1.

When we subtract these two expressions and simplify, what do we get?
当我们减去这两个表达式并进行简化时，我们会得到什么？

B−B∗2+I−I∗−22B−B∗​+I−I∗−2

B−B∗2+I−I∗2B−B∗​+I−I∗

B+B∗2+I−I∗+22B+B∗​+I−I∗+2

B+B∗2+I−I∗2B+B∗​+I−I∗

We have 我们有

Q=B+B∗,R=I−B∗−I∗.Q=B+B∗,R=I−B∗−I∗.

Now we can use substitution to put the above equalities into the expression below and write it in terms of QQ and R:R:
现在我们可以使用替换将上述等式放入下面的表达式中，并用 QQ 和 R:R: 来写

B−B∗2+I−I∗.2B−B∗​+I−I∗.

The first equation can be written as B=Q−B∗.B=Q−B∗. What’s the result of that substitution?
第一个方程可以写成 B=Q−B∗.B=Q−B∗. 那个替换的结果是什么？

Q2−R+22Q​−R+2

Q2+R2Q​+R

Q2+R+12Q​+R+1

Q2+2R2Q​+2R

Explanation 解释

We need to express this in terms of QQ and R:R:
我们需要用 QQ 和 R:R: 来表达这一点

B−B∗2+I−I∗.2B−B∗​+I−I∗.

Substitute Q−B∗Q−B∗ for B:B:
将 Q−B∗Q−B∗ 替换为 B:B:

Q−B∗−B∗2+I−I∗.2Q−B∗−B∗​+I−I∗.

Combine like terms: 组合 like terms：

Q−2B∗2+I−I∗.2Q−2B∗​+I−I∗.

Distribute the division: 分配分区：

Q2−B∗+I−I∗.2Q​−B∗+I−I∗.

Rearranging, we notice the last three terms are just R:R:
重新排列，我们注意到最后三个术语只是 R:R:

Q2+R.2Q​+R.

Compare the original Pick’s formula
比较原始 Pick 的公式

B2+I−12B​+I−1

with the new one 与新的

Q2+R,2Q​+R,

where QQ is the number of boundary points on the combined polygon and RR is the number of interior points on the combined polygon.
其中 QQ 是组合多边形上的边界点数， RR 是组合多边形上的内部点数。

Because we did this generally, this works with any figure with a single hole in it. Trying it on the figure below gets an area of 12:12:
因为我们通常这样做，所以这适用于_任何_带有单个孔的图形。在下图上尝试得到 12:12: 的面积

242+0=12.224​+0=12.

What’s the area of the figure in square units, excluding the hole inside?
不包括里面的孔，以平方单位表示的数字面积是多少？

2525

2626

2727

2828

2929

3030

Explanation 解释

The outer portion has 44 boundary points, and the hole touches at 66 points, making Q=4+6=10.Q=4+6=10.
外部有 44 边界点，孔在 66 点接触，使 Q=4+6=10.Q=4+6=10.

The interior points are marked below, that is, R=23:R=23:
内部点在下面标记，即 R=23:R=23:

By the formula, the area of the figure is 102+23=5+23=28210​+23=5+23=28 square units.
根据公式，该图的面积为 102+23=5+23=28210​+23=5+23=28 平方单位。

So far, we’ve stuck to having only one hole to worry about — what if there are many holes? What happens to the formula then?
到目前为止，我们一直坚持只有一个漏洞需要担心 —— 如果有很多漏洞怎么办？那么公式会怎样呢？

It turns out to be quite elegant — try the last lesson and find out what happens.
事实证明，它非常优雅 — 尝试最后一节课，看看会发生什么。

Pick’s Theorem with Multiple Holes

具有多个孔的 Pick 定理

We’re about to figure out Pick’s theorem using a polygon with any number of holes. Be warned, while only ordinary algebra is used and the end result is amazingly simple, this set is more challenging than the other parts of the course.
我们即将使用具有任意数量孔的多边形来计算 Pick 定理。请注意，虽然只使用普通代数并且最终结果非常简单，但这套课程比课程的其他部分更具挑战性。

HH will be the number of holes. For example, on the diagram below, H=4.H=4.
HH 将是孔数。例如，在下图中， H=4.H=4.

BB is still the number of boundary points on the original polygon, and II is the number of interior points on the original polygon:
BB 仍然是原始多边形上的边界点数， II 是原始多边形上的内部点数：

When we write B∗,B∗∗,B∗∗∗,…,B∗,B∗∗,B∗∗∗,…, assume B∗B∗ stands for the number of boundary points on the first hole, B∗∗B∗∗ stands for the number of boundary points on the second hole, and so forth.
当我们写 B∗,B∗∗,B∗∗∗,…,B∗,B∗∗,B∗∗∗,…, 时，假设 B∗B∗ 代表第一个洞的边界点数， B∗∗B∗∗ 代表第二个洞的边界点数，依此类推。

The same applies for I∗,I∗∗,I∗∗∗,…,I∗,I∗∗,I∗∗∗,…, except using interior points.
这同样适用于 I∗,I∗∗,I∗∗∗,…,I∗,I∗∗,I∗∗∗,…, ，但使用内部点除外。

What’s I∗+I∗∗+I∗∗∗+I∗∗∗∗I∗+I∗∗+I∗∗∗+I∗∗∗∗ on the diagram above?
上图中的 I∗+I∗∗+I∗∗∗+I∗∗∗∗I∗+I∗∗+I∗∗∗+I∗∗∗∗ 是什么？

00

11

22

33

44

Explanation 解释

Every hole only has boundary points with no interior points, so the sum of all the interior points of the holes is 0.0.
每个孔只有边界点，没有内部点，因此所有孔的内部点之和为 0.0.

To make things easier to read, whenever we have
为了让事情更容易阅读，无论何时我们都有

B∗+B∗∗+B∗∗∗+⋯,B∗+B∗∗+B∗∗∗+⋯,

we’ll now write (sum of hole boundary points).(sum of hole boundary points). Whenever we have
我们现在写 (sum of hole boundary points).(sum of hole boundary points). 每当我们有

I∗+I∗∗+I∗∗∗+⋯,I∗+I∗∗+I∗∗∗+⋯,

we’ll now write (sum of hole interior points).(sum of hole interior points).
我们现在写 (sum of hole interior points).(sum of hole interior points).

Now we’re going to lead to a big calculation — we’re going to make the combined polygon with the outer polygon with every hole on the inside, no matter how large H,H, the number of holes, is.
现在我们将进行一个大的计算 — 我们将使用外部多边形的组合多边形，每个孔都在内部，无论 H,H, 的孔数有多大。

Q,Q, the number of boundary points on the combined polygon, is the same as that of the outer polygon, except all the boundary points from the holes now are boundary points of the combined polygon — that is,
Q,Q, 组合多边形上的边界点数量 与外部多边形的边界点数量相同，只是 洞中的所有边界点现在都是组合多边形的边界点——即

Q=B+(sum of hole boundary points).Q=B+(sum of hole boundary points).

R,R, the number of interior points on the combined polygon, is the same as that of the outer polygon, except all boundary points and interior points from the holes are removed.
R,R, 组合多边形上的内部点数 与外部多边形的相同，只是去除了孔中的所有边界点和内部点。

What does RR equal?
RR 等于什么 ？

I−(sum of hole boundary points)−(sum of hole interior points)I​−(sum of hole boundary points)−(sum of hole interior points)​

I−(sum of hole boundary points)+(sum of hole interior points)I​−(sum of hole boundary points)+(sum of hole interior points)​

I+(sum of hole boundary points)+(sum of hole interior points)I​+(sum of hole boundary points)+(sum of hole interior points)​

Explanation 解释

We want to start with the interior points of the outer polygon
我们想从外部多边形的内部点开始

I,I,

and subtract the exterior and interior points of all the holes, since they are getting removed from the total.
并 减去 所有孔的外部点和内部点，因为它们将从总数中删除。

Each and every individual area of the outer polygon or hole is B2+I−1,2B​+I−1, with some number of stars added indicating a particular hole.
外部多边形或孔的每个单独区域都是 B2+I−1,2B​+I−1, ，并添加了一些星星来表示特定的孔。

We want to start with the outer polygon area B2+I−12B​+I−1 and subtract all the holes:
我们想从外部多边形区域 B2+I−12B​+I−1 开始，减去所有孔：

(B2+I−1)−(B∗2+I∗−1)−(B∗∗2+I∗∗−1)−⋯.(2B​+I−1)−(2B∗​+I∗−1)−(2B∗∗​+I∗∗−1)−⋯.

When we do the subtraction, we get one set of “boundary” terms
当我们进行减法时，我们会得到一组 “边界” 项

B−(sum of hole boundary points)22B−(sum of hole boundary points)​

added to a set of “interior” terms
添加到一组 “interior” 术语中

I−(sum of hole interior points)I−(sum of hole interior points)

and to some “11” terms:
以及一些 “ 11 ” 术语：

−1+1+1+1+⋯.−1+1+1+1+⋯.

When the “11” terms are combined, what’s the result?
当 “ 11 ” 术语组合在一起时，结果是什么？

Remember, HH is the number of holes.
请记住， HH 是孔数。

H−2H−2

H−1H−1

HH

H+1H+1

Explanation 解释

Looking back at 回头看

(B2+I−1)−(B∗2+I∗−1)−(B∗∗2+I∗∗−1)−⋯,(2B​+I−1)−(2B∗​+I∗−1)−(2B∗∗​+I∗∗−1)−⋯,

the number of actual terms starting from (B∗2+I∗−1)(2B∗​+I∗−1) is just the number of holes. That is,
从 (B∗2+I∗−1)(2B∗​+I∗−1) 开始的实际项数 只是孔数。那是

• (B∗2+I∗−1)(2B∗​+I∗−1) is hole number 1,1,
  (B∗2+I∗−1)(2B∗​+I∗−1) 是孔号 1,1,

• (B∗∗2+I∗∗−1)(2B∗∗​+I∗∗−1) is hole number 2,2,
  (B∗∗2+I∗∗−1)(2B∗∗​+I∗∗−1) 是孔号 2,2,

• (B∗∗∗2+I∗∗∗−1)(2B∗∗∗​+I∗∗∗−1) is hole number 3,3,
  (B∗∗∗2+I∗∗∗−1)(2B∗∗∗​+I∗∗∗−1) 是孔号 3,3,

• etc. 等。

Focusing on just the “11” terms, we have
仅关注 “ 11 ” 术语，我们有

−1+1+1+1+⋯,−1+1+1+1+⋯,

where we start at −1−1 and the number of 11s being added is equal to the number of holes. This is the same as −1+H,−1+H, or H−1.H−1.
其中我们从 −1−1 开始，添加的 11 的数量等于孔的数量。这与 −1+H,−1+H, 或 H−1.H−1. 相同

Our goal will be to write our formula in terms of
我们的目标是根据

• Q,Q, the boundary points of the combined polygon,
  Q,Q, 组合多边形的边界点，

• R,R, the interior points of the combined polygon, and
  R,R, 组合多边形的内点，以及

• H,H, the number of holes.
  H,H, 孔数。

Our working formula has a “boundary points” term
我们的工作公式有一个 “boundary points” 项

B−(sum of hole boundary points)22B−(sum of hole boundary points)​

added to an “interior points” term
已添加到 “Interior Points” 术语

I−(sum of hole interior points)I−(sum of hole interior points)

and to a 11s term that we just determined was
以及 我们刚刚确定的 11 s 术语

H−1.H−1.

Using the 使用

R=I−(sum of hole boundary points)−(sum of hole interior points)R=I​−(sum of hole boundary points)−(sum of hole interior points)​

equation given earlier in the lesson, what can we turn the “interior points” term into?

 R−(sum of hole interior points) R−(sum of hole interior points) R+(sum of hole interior points) R+(sum of hole interior points) R−(sum of hole boundary points) R−(sum of hole boundary points) R+(sum of hole boundary points) R+(sum of hole boundary points)

Explanation 解释

We have 我们有

R=I−(sum of hole boundary points)−(sum of hole interior points).R=I​−(sum of hole boundary points)−(sum of hole interior points).​

Add the sum of hole boundary points to both sides of the equal sign:
将孔边界点与等号两侧的总和相加：

R+(sum of hole boundary points)=I−(sum of hole interior points).​R+(sum of hole boundary points)=I−(sum of hole interior points).​

Look at the “interior points” term of our working formula:
看看 我们工作公式的 “interior points” 项：

I−(sum of hole interior points).I−(sum of hole interior points).

This is the same as the right side of the equality. So it’s equivalent to
这与相等的右侧相同。所以它相当于

R+(sum of hole boundary points).R+(sum of hole boundary points).

Again, remember, our goal will be to write the area of the combined polygon in terms of
同样，请记住，我们的目标是用

• Q,Q, the boundary points of the combined polygon,
  Q,Q, 组合多边形的边界点，

• R,R, the interior points of the combined polygon, and
  R,R, 组合多边形的内点，以及

• H,H, the number of holes.
  H,H, 孔数。

We still have the “boundary points” term
我们仍然有 “boundary points” 项

B−(sum of hole boundary points)22B−(sum of hole boundary points)​

added to the remaining terms
添加到其余条款

R+(sum of hole boundary points)+H−1.R+(sum of hole boundary points)+H−1.

Using 用

Q=B+(sum of hole boundary points)Q=B+(sum of hole boundary points)

from earlier in the lesson, we can do a substitution and find our final formula. What is it?
从本课的前面部分开始，我们可以进行替换并找到最终公式。这是什么？

Q2−R+H−12Q​−R+H−1

Q+R2+R+H−12Q+R​+R+H−1

Q2+R+H−12Q​+R+H−1

Q−R2+R+H−12Q−R​+R+H−1

Explanation 解释

Starting with 起始

Q=B+(sum of hole boundary points),Q=B+(sum of hole boundary points),

isolate the BB term
隔离 BB 项

B=Q−(sum of hole boundary points)B=Q−(sum of hole boundary points)

and then substitute into  ，然后替换为

B−(sum of hole boundary points)2,2B−(sum of hole boundary points)​,

which gives 这样得到

Q−2⋅(sum of hole boundary points)2.2Q−2⋅(sum of hole boundary points)​.

Distributing the division, this is equal to
分配除法，这等于

Q2−(sum of hole boundary points).2Q​−(sum of hole boundary points).

Now we can combine this together with the remaining terms:
现在我们可以将其与其余项组合在一起：

Q2−(sum of hole boundary points)+R+(sum of hole boundary points)+(H−1).2Q​​−(sum of hole boundary points)+R+(sum of hole boundary points)+(H−1).​

The two boundary point sums cancel, leaving
两个边界点 sum 取消，留下

Q2+R+H−1.2Q​+R+H−1.

Comparing the formula we just obtained with the original version of Pick’s theorem, we find that they’re nearly the same. The only difference is that now we add the number of holes.
将我们刚刚获得的公式与 Pick 定理的原始版本进行比较，我们发现它们几乎相同。唯一的区别是现在我们 添加了孔的数量。

Let’s apply it one last time.
让我们最后一次应用它。

What’s the area of the figure above?
上图的面积是多少？

Explanation 解释

There are 2828 boundary points and 77 interior points, as well as 33 holes:
有 2828 边界点和 77 内部点，以及 33 孔：

282+7+3−1=14+9=23.228​+7+3−1=14+9=23.